这叫推理吗?还以为怎么回事呢,看到Next, we expand the product觉得果然,顶多也就这样了吧。 我来讲讲什么叫一般规律,什么叫数学。
得到 f_1(x)=x,f_2(x)=x(x+1)/2,f_3(x)=x(x+1)(x+2)/6……之后,很容易猜想 f_n(x)=x(x+1)(x+2)...(x+n-1)/n! 怎么证明呢? 显然用数学归纳法。假设f_k(x)=x(x+1)(x+2)...(x+k-1)/k!,那么是否有 \sum _{i=1}^x f_k(i) = f_{k+1}(x)? 为了让问题直观,可以把f_k(x)改写为 f_k(x)= (x+k-1)! / ( (x-1)!k! ) = \binom{x+k-1}{k} 所以就是要证明 \sum_{i=1}^x \binom{i+k-1}{k} = \binom{x+k}{k+1}
直观一点显示,就是 从 二项分布三角形的第 k 行 第 k 个数开始,加上下一行的第k个数,再加上下一行的……直到第 x+k-1 行为止,是否等于第 x+k 行的第 k+1 个数。 以图片为例,

就是要证明 从最右边的那一列 1 随便选一个,往左下累加,那不管到哪里停住,其和一定等于停住的地方的右下角的数。(比如此图上 1+3+6+10+15 = 35) 证明其实很简单,
(给想独立思考的人留出的空白分割线) ——————————————————————————
把第一个1等价到右下的1,看作这样
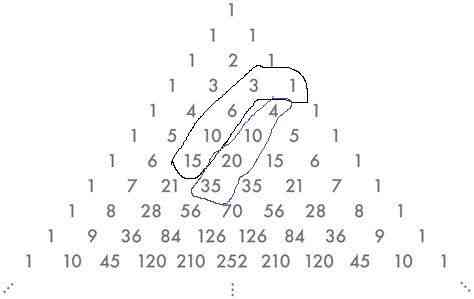
那么根据二项分布的特性,1+3变成下面的4,+6变成下面的10,以此类推,显然最后会落在末尾数字的右下角。得证。 这才是数学的思路。

