语言模型输出端共享Embedding的重新探索

2023-07-26 16:07

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 科学空间

研究方向 | NLP、神经网络

预训练刚兴起时，在语言模型的输出端重用 Embedding 权重是很常见的操作，比如 BERT、第一版的 T5、早期的 GPT，都使用了这个操作，这是因为当模型主干部分不大且词表很大时，Embedding 层的参数量很可观，如果输出端再新增一个独立的同样大小的权重矩阵的话，会导致显存消耗的激增。

不过随着模型参数规模的增大，Embedding 层的占比相对变小了，加之《Rethinking embedding coupling in pre-trained language models》[1] 等研究表明共享 Embedding 可能会有些负面影响，所以现在共享 Embedding 的做法已经越来越少了。

本文旨在分析在共享 Embedding 权重时可能遇到的问题，并探索如何更有效地进行初始化和参数化。尽管共享 Embedding 看起来已经“过时”，但这依然不失为一道有趣的研究题目。

共享权重

在语言模型的输出端重用 Embedding 权重的做法，英文称之为 “Tied Embeddings” 或者 “Coupled Embeddings”，其思想主要是 Embedding 矩阵跟输出端转换到 logits 的投影矩阵大小是相同的（只差个转置），并且由于这个参数矩阵比较大，所以为了避免不必要的浪费，干脆共用同一个权重，如下图所示：

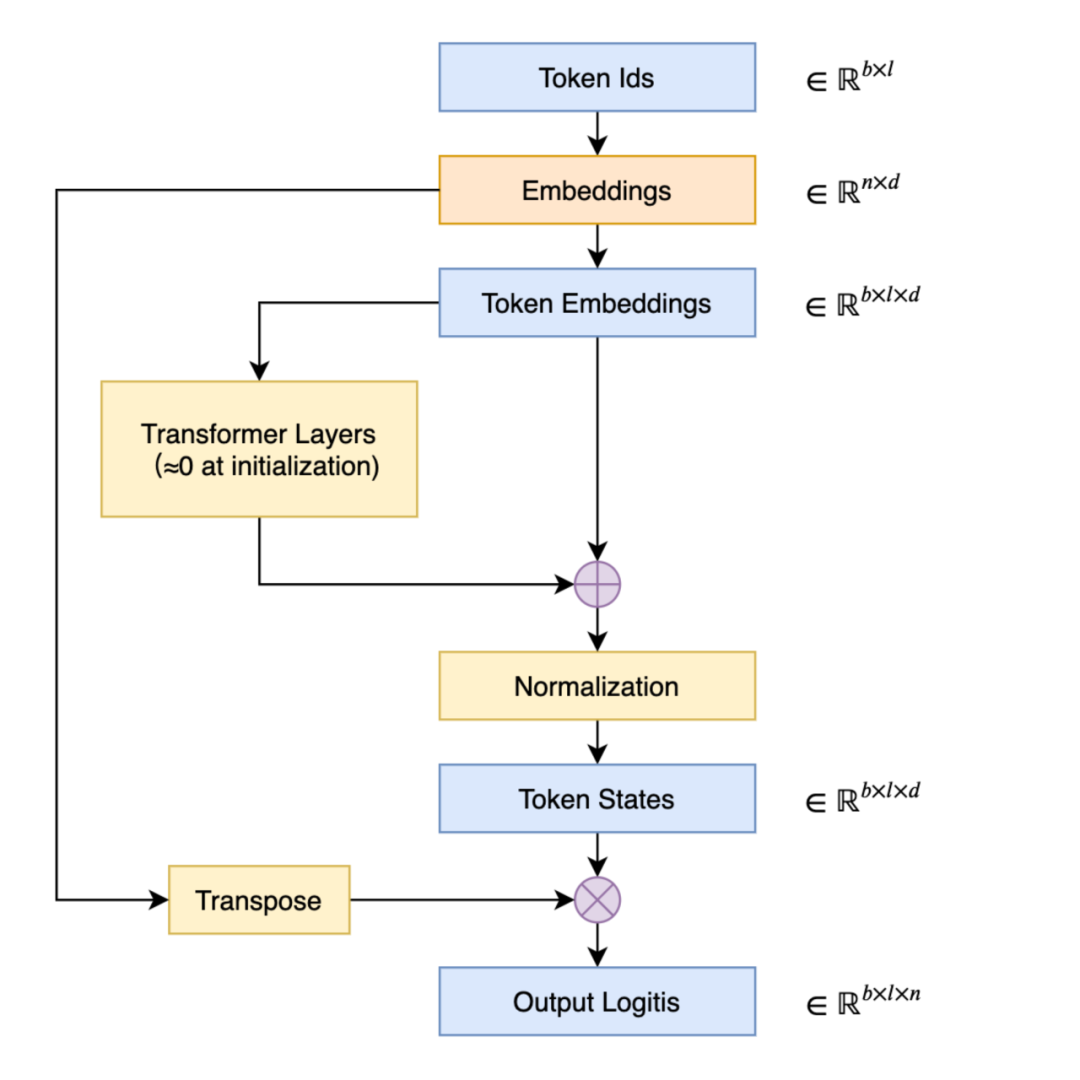
▲ 共享 Embedding 权重的 Transformer 示意图

共享 Embedding 最直接的后果可能是——它会导致预训练的初始损失非常大。这是因为我们通常会使用类似 DeepNorm 的技术来降低训练难度，它们都是将模型的残差分支初始化得接近于零。换言之，模型在初始阶段近似于一个恒等函数，这使得初始模型相当于共享 Embedding 的 2-gram 模型。接下来我们将推导这样的 2-gram 模型损失大的原因，以及分析一些解决方案。

准备工作

在正式开始推导之前，我们需要准备一些基础结论。

首先，要明确的是，我们主要对初始阶段的结果进行分析，此时的权重都是从某个“均值为 0、方差为 ”的分布中独立同分布地采样出来的，这允许我们通过期望来估计某些求和结果。比如对于，我们有

因此可以取。那么误差有多大呢？我们可以通过它的方差来感知。为此，我们先求它的二阶矩：

如果采样分布是正态分布，那么可以直接算出，所以

这个方差大小也代表着的近似程度，也就是说原本的采样方差越小，那么近似程度越高。特别地，常见的采样方差是（对应，即单位向量），那么代入上式得到，意味着维度越高近似程度越高。此外，如果采样分布不是正态分布，可以另外重新计算，或者直接将正态分布的结果作为参考结果，反正都只是一个估算罢了。

如果是另一个独立同分布向量，那么我们可以用同样的方法估计内积，结果是

以及

同样地，取的话，那么方差是，维度越高近似程度越高。以上两个结果可以说是《n维空间下两个随机向量的夹角分布》[2]、《让人惊叹的Johnson-Lindenstrauss引理：理论篇》中的结论的统计版本。

损失分析

对语言模型来说，最终要输出一个逐 token 的元分布，这里是词表大小。假设我们直接输出均匀分布，也就是每个 token 的概率都是，那么不难计算交叉熵损失将会是。这也就意味着，合理的初始化不应该使得初始损失明显超过，因为代表了最朴素的均匀分布，明显超过等价于说远远不如均匀分布，就好比是故意犯错，并不合理。

那么，为什么共享 Embedding 会出现这种情况呢？假设初始 Embedding 是，前面已经说了，初始阶段残差分支接近于零，所以输入输入 token ，模型输出就是经过 Normalization 之后的 Embedding 。常见的 Normalization 就是 Layer Norm 或者 RMS Norm，由于初始化分布是零均值的，所以 Layer Norm 跟 RMS Norm 大致等价，因此输出是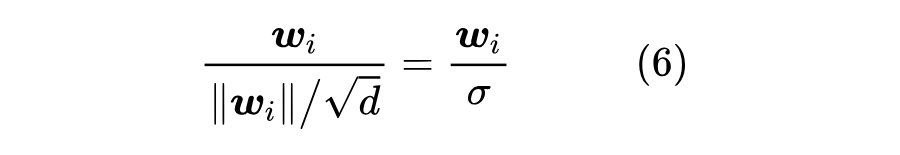

接下来重用 Embedding，内积然后 Softmax，所建立的分布实质是

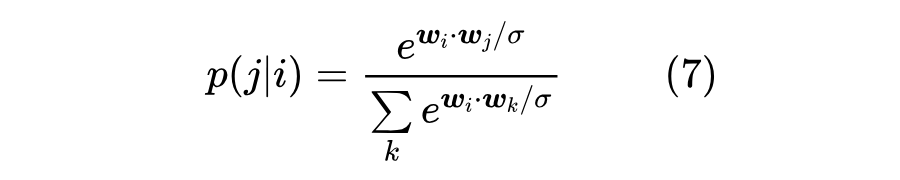
对应的损失函数就是

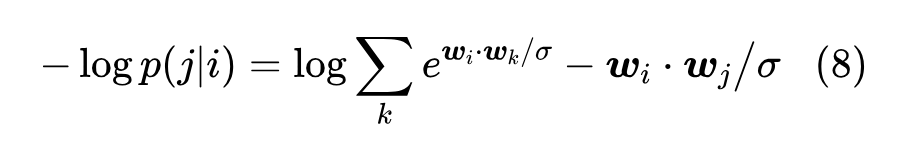
语言模型任务是为了预测下一个 token，而我们知道自然句子中叠词的比例很小，所以基本上可以认为，那么根据结果 (4) 就有。所以，初始损失函数是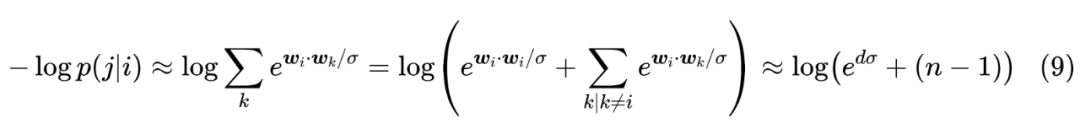

后面的再次用到了式（1）和式（4）。常见的初始化方差，或者是一个常数，或者是（此时），不管是哪一种，当较大时，都导致占主导，于是损失将会是级别，这很容易就超过了均匀分布的。

一些对策

根据上述推导结果，我们就可以针对性地设计一些对策了。比较直接的方案是调整初始化，根据式（9），我们只需要让，那么初始损失就是变成级别的，也就是说初始化的标准差要改为。

一般来说，我们会希望参数的初始化方差尽量大一些，这样梯度相对来说没那么容易下溢，而有时候会显得过小了。为此，我们可以换一种思路：很明显，式（9）之所以会偏大，是因为出现了，由于两个相同，它们内积变成了模长，从而变得很大，如果能让它们不同，那么就不会出现这一个占主导的项了。

为此，最简单的方法自然是干脆不共享 Embedding，此时是而不是，用（4）而不是（1）作为近似，于是式（9）渐近于。如果还想保留共享 Embedding，我们可以在最后的 Normalization 之后，再接一个正交初始化的投影层，这样变成了，根据 Johnson-Lindenstrauss 引理，经过随机投影的向量近似于独立向量了，所以也近似于不共享的情况，这其实就是 BERT 的解决办法。特别地，这个投影层还可以一般化地加上 bias 和激活函数。

如果一丁点额外参数都不想引入，那么可以考虑在 Normalization 之后“打乱” 的各个维度，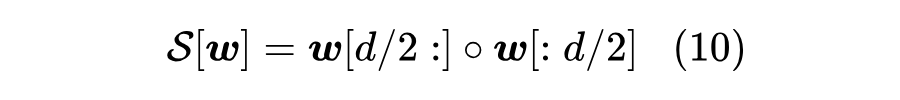

这里的是拼接操作，那么和也接近正交了，内积自然也约等于0。这相当于（在初始阶段）将原来的的 Embedding 矩阵劈开为两个的矩阵然后构建不共享 Embedding 的 2-gram 模型。另外，我们还可以考虑其他打乱操作，比如 ShuffleNet [3] 中的先 reshape，然后 transpose 再 reshape 回来。

在笔者的实验中，直接改初始化标准差为收敛速度是最慢的，其余方法收敛速度差不多，至于最终效果，所有方法似乎都差不多。