【新智元导读】疯狂入坑AI工具的数学大神陶哲轩，最近又被Lean4和Copilot震惊了——它们竟然帮他发现了自己论文中的一处错误！2026年AI成为数学论文合著者的预言，已经愈发逼近了。
最近，热衷于用GPT-4、Copilot做研究的数学大神陶哲轩，又在AI的帮助下发现了自己论文中的一处隐藏bug！陶哲轩表示，自己在用Lean4形式化第6页论点的过程中发现，表达式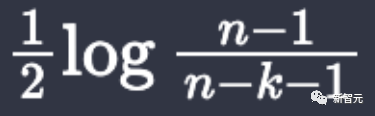
在n=3,k=2时，实际上是发散的。这个不太容易看出的bug能被及时捉住，多亏了Lean4。原因是，Lean要求他构建0<n−3，但陶哲轩只假设了n>2。由此，Lean无法基于负的0<n−3得到反证。好在，这只是一个小bug，只存在于n值很小的情况。此时，只需修改论文中的一些常数就可以了。一些数学爱好者粉丝在此帖中惊呼：这太惊人了，很高兴看到AI证明助手的传播，为数学研究的未来奠定了更坚实的基础。或许在不久的将来，我们就可以在Lean之上构建一个AI层。只要把证明中的各步描述给AI，AI就可以利用Lean来执行证明了，过程中还能各种调用计算机代数软件包。
今年6月，陶哲轩就曾在GPT-4试用体验的博客中预言——2026年，AI将与搜索和符号数学工具相结合，成为数学研究中值得信赖的合著者。
而陶哲轩也身体力行，新论文已经开始用GPT-4写了，并屡屡惊呼——GitHub Copilot的惊人能力，让我感到不安！
在GPT-4的帮助下，他开始学习用Lean4写论文、做数学研究。这个过程无疑令他十分激动，因此隔三岔五（甚至每隔几个小时）就会在mastodon上发帖，记录自己的学习感悟和经验总结。在写一篇关于麦克劳林不等式研究的论文中，陶哲轩就大量用到了GPT-4、Copilot、Lean4等AI工具。
论文地址：https://arxiv.org/abs/2310.05328现在的进度是，陶哲轩已经在Lean4中完成对论文第2节论点的修复了。只不过这个过程这比他预想的要繁琐得多，每一行证明都要花费大约一个小时来形式化。在项目的第一周，他的瓶颈在于不熟悉Lean语法和工具；但目前的瓶颈在于工具本身——不如计算机代数软件包中的工具先进。假设所有分母都是正数，这对于人工计算来说是一项非常快速的任务，在任何标准的计算机代数软件包中也能相当容易地完成。Lean虽然有着非常实用的自动工具来处理线性运算，但目前还没有自动简化涉及指数复杂表达式的工具。因此，我们必须一步一步地处理指数定律以及上述其他运算，而这个过程非常耗时。最后，陶哲轩决定不在这部分论证中使用渐进符号，而是建立了一个带有确定常数C的不等式：最开始，陶哲轩认为用诸如C=7这样的值来证明不等式会「更简单」。但利用现有工具去严格证明C≤7非常繁琐，于是就放弃了这个想法，转而使用形式上更可操作的C值。现在所选的，数值大约为6.16。对此，有好奇的网友问道：「与手算相比，AI在证明速度方面做得如何？」陶哲轩表示，根据自己的观察，那些对计算机代数软件包和计算器来说是机械性的任务类型，对形式化证明助手来说未必是机械性的。但随着LLM的出现，我们应该可以将所有的计算机辅助工具统一成一个对用户非常友好的通用工具。而这个工具将拥有每个组件的全部优点。甚至，在不久的将来，我们还可以设想在Lean之上构建一个AI层——通过「数学英语」将证明中的各个步骤描述给AI，然后AI就可以尝试利用Lean来执行，或许在这个过程中还能调用计算机代数软件包。
此前，在这篇麦克劳林不等式研究的论文中，陶哲轩就惊诧地发现，Copilot竟然能够预测出自己下一步想要做什么！它不仅能正确预测出用于各种例行验证的多行代码，还能根据陶哲轩提供定理的名称，推断出他想要往哪个方向做研究。在证明论文定理1.3的过程中，陶哲轩用Lean4完成了定理证明的形式化。在论文中，证明过程中只有一页纸，不过形式化证明却使用了200行Lean4。比如在论文中，陶哲轩只是假定
在任何a>0的实数上都是凸的，并在之后调用了詹森不等式。但相关代码却需要差不多50行。在这个过程中，GitHub Copilot表现出了种种神预测，神奇地推测出了陶哲轩的研究接下来的方向。而Lean的重写策略，让他能通过有针对性的替换，来修改冗长的假设或目标。这个功能极为重要，它可以让人们自由操纵这些表达式，而不必总是完整地输入它们。陶哲轩表示自己需要粗略地模拟Lean4的重写策略，通过剪切、粘贴等操作，对从一行到下一行的冗长表达式进行有针对性的编辑。这会导致错别字在文档中一连传播多行。而Lean4就能以自动和验证的方式，完成这种重写。当然，Lean 4目前还不是万能的，也存在一些局限。比如重写涉及约束变量的表达式，并不总能轻易完成。陶哲轩表示自己很期待，什么时候很简单地用自然语言，来要求LLM进行这样的转换。入坑GPT-4+GitHub Copilot，疯狂安利
早在9月初，陶哲轩就曾发帖大赞ChatGPT生成Python代码的效果——直接节省了半小时的工作量！作为实验，他要求ChatGPT写一段Python代码，为每个自然数n计算1,...,n的最长子序列的长度𝑀(𝑛) ，其中欧拉全能函数ϕ不递减。例如，𝑀(6)=5，因为ϕ在1,2,3,4,5（或 1,2,3,4,6）上是非递减的，但在 1,2,3,4,5,6 上不是。有趣的是，它生成了一段极其巧妙的代码来计算全能函数，这段代码如此之巧妙，以至于陶哲轩不得不盯着它看了几分钟，才明白代码背后的原理究竟是什么。当然，这段代码也存在偏差——它只考虑了连续整数的子序列，而不是任意子序列。不过，这已经足够接近了，用ChatGPT生成的这段初始代码作为起点，陶哲轩最终手动生成了自己想要的代码，这大概节省了他半个小时的工作量。由于ChatGPT给出的结果非常好，陶哲轩表示，自己以后还会经常使用它，为类似的计算提供初始代码。很快，陶哲轩又发帖表示，自己已经在网友的推荐下入坑GitHub Copilot了！不出所料，Copilot随后的表现着实让他喜出望外——只给了开头一段外加一句话，AI就推荐了和自己的构想非常接近的内容。陶哲轩只需对这些建议稍作修改，就可以用不到原计划一半的时间完成了。时间来到10月，陶哲轩在进行自然数游戏研究时发现，虽然GPT-4不能为游戏提供直接的帮助，但当他开始使用Lean时，GPT-4就变得非常有用了。随着关卡变得越来越难，GPT的作用开始逐渐显现出来。在Z显而易见是X和Y的结果的情况下，向GPT提问「如果我已经知道X和Y，该如何证明Z呢」，就可以解决过程中各种微妙的语法问题。除了专业相关的内容，陶哲轩在发现自己可以用DALL·E 3之后，就立刻玩了起来。
大神在数学研究中如此痴迷AI工具，也引起了网友们的热议。有人表示 ，大神是在本月初在GPT-4帮助下开始学习Lean4的，不时就会在mastodon上随手记录下自己的学习进展。这也说明，对于最成功的人，LLM都能加速他们的工作。
有人表示，即使不会写代码的人，只要是一个优秀的LLM沟通者，都能快速实现功能的自动化。
不过，如果只有高技能人才才能有效利用LLM的话，结果就是可能会加剧人与人之间的不平等。
马上有人现身说法表示，是这样的，自己的朋友此前除了Excel公式外不会写任何东西，但现在，他已经能用GPT-4编写Python应用程序了！
而自己作为拥有30年开发经验的码农，还需要恳求他教一教自己这项技术。
他的成功，大概就是因为他很会和LLM沟通。
有人预言，随着时间的推移，使用LLM的人会获得压倒性的好处，无论本身智力如何，他们都将在梯子上越爬越高，成为考试专家。
对于精英来说，他们或许会从LLM那里得到100倍的助力，而对于顶级工程师，这种助力大概能有10000倍。
