丘成桐被《纽约客》“污名”以及佩雷尔曼证明“庞加莱猜想”

2006年8月28日《纽约客》杂志上有一篇文章叫“流形的命运”。文章讲的是数学界在证明“庞加莱猜想”过程中的一些事件。主要人物是目前公认的证明者格里戈里·佩雷尔曼以及几何拓扑领域的大师丘成桐。
这篇文章之所以对中国读者特别有趣，是因为它给丘成桐这位1982年菲尔茨奖得主描绘了一幅难看的肖像。在佩雷尔曼发表他的证明之后，丘成桐极力推荐他的学生和同事曹怀东和朱熹平发表他们的证明，并声称这两个人是最先实质证明了这个猜想的人。因为数学界公认最困难最关键的部分由佩雷尔曼破解，后来人做的没有特殊贡献，因此丘成桐似乎有意掠夺猜想证明的功绩。文章中也谈及丘成桐对他的学生田刚进行攻击的事情。文章发表后，丘成桐表示要采取法律行动，不过后来似乎也不了了之了。曹怀东和朱熹平野修改了他们的文章，更好地说明了一些受到争议的部分。

文章写的有声有色，因为该文的主要作者，Sylvia Nasar，是我们熟知的写《美丽心灵》约翰纳什的那个人。
不过读后，我倒是对佩雷尔曼这个人的故事感兴趣，觉得应该给读者们介绍一下。丘成桐的事次要。
首先说说庞加莱猜想是什么，因为这个猜想现在已经被证明了，就是庞加莱定理了。
如果用数学语言严格来说，庞加莱猜想是这样的：任一单连通的、封闭的三维流形与三维球面同胚。
用非数学语言来说就是：每一个没有洞的封闭三维物体，都“等价”于一个三维的球面。这里说的等价是拓扑意义上的，不过我们不需深究。
“单连通“指的是没有洞。粗浅的比喻是：把一个橡皮筋围绕在一个像柳橙一样东西的表面，因为可以既不扯断它，也不让它离开表面，就可以使它慢慢移动并收缩为一个点；那么柳橙这样的东西，它的表面就是“单连通的”。与此对比，同样的橡皮筋套在一个甜甜圈上，有些皮筋在不离开表面的情况下怎么收缩也不能成为一个点，除非扯断橡皮筋或者甜甜圈。因此，甜甜圈那样的东西，它的表面不是“单连通的”。

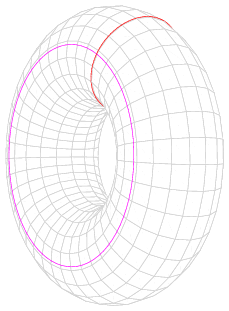
图中环面上两个上色的圆均无法连续地收紧成一点。因此环面就不与球面同胚。
自1904年庞加莱猜想被提出来以后，很多人都试图解决它。有趣的是，三维以上，也就是四维，五维的情况，到八十年代就被证明了，但是三维却没有。于是庞加莱猜想也就是一个关于三维球体特征的难题。由于它对数学和物理尤其是宇宙学都有着重要的意义，而且多年来都迟迟未能被解开，被视为非常重要的问题之一。
也许有人想知道这个猜想为什么那么重要，但内容太多，我们今天就掠过不说了，还是讲故事重要。
故事的主人公佩雷尔曼是个俄国犹太人，可以说是人们能想象的典型数学家，虽然现实生活中可能没有几个这样的。解决了这个问题之后，丘成桐得到的菲尔茨奖，它的委员会也决定把这个数学界最高名誉奖项颁给佩雷尔曼，但他拒绝了，他说， “每个人都明白，如果证明是正确的，就不需要其他认可的方式。” 另外一个叫克雷数学研究所的本来就是要给解决这个问题的人一百万美元奖金的，他也拒绝了。2005年，佩雷尔曼辞去了他一直工作的俄国斯特克洛夫数学研究所的研究工作，2006年又表示对数学领域的道德标准感到失望，退出专业数学研究。现在他隐居在圣彼得堡，自 2006 年以来一直没有再接受采访。
你可以说他不食人间烟火，但也许一个纯粹的数学家真不需要这些。
佩雷尔曼的父亲是一名电气工程师，一直鼓励他对数学产生兴趣。“他让我思考逻辑和其他数学问题。买了很多书给我读。教我下棋，也为我骄傲。”他父亲送给他的书中有一本是《娱乐物理学》，这本书在十九世纪三十年代是苏联的畅销书。在前言中，作者将内容描述为“难题、脑筋急转弯、有趣的轶事和意想不到的，大量引用儒勒·凡尔纳、H·G·威尔斯、马克·吐温和其他作家的观点，因为，除了提供娱乐，这些作者描述的奇妙实验很可能成为物理课上的指导性插图。”这本书的主题包括如何从行驶中的汽车上跳下来安全，为什么“根据浮力定律，我们永远不会在死海淹死。” 也许有点像中国的《十万个为什么》。
十四岁的时候，他已成为当地数学俱乐部的明星。1982年，丘成桐获得菲尔兹奖时，佩雷尔曼在布达佩斯举行的国际数学奥林匹克竞赛中获得满分并获得金牌。他是同年级的两三个犹太人之一，对歌剧充满热情，这也使他在同龄人中很不寻常。他母亲是一所技术学院的数学老师，拉小提琴，在他六岁时开始带他去看歌剧。佩雷尔曼十五岁时，他开始把零用钱花在唱片上，很高兴能拥有一张 1946 年著名的《茶花女》的唱片，尤其喜欢莉西亚·阿尔巴内塞 (Licia Albanese) 饰演维奥莱塔 (Violetta)。“她的声音非常好听，”他说。
1982年，16岁的佩雷尔曼进入列宁格勒大学学习几何学，在学校里表现优异，解决了斯特克洛夫研究所数学家尤里·布拉戈 (Yuri Burago) 提出的问题，后者后来就成为佩雷尔曼的博士学位导师。 “有很多能力很强的学生，先说后想，”布拉戈说。“格里沙不同。他想问题很深。他的回答总是正确的，也总是非常仔细地检查。”布拉戈补充道：“他解决问题的速度不快。速度没有任何意义。数学并不取决于速度，而在深度。”
九十年代初，在斯特克洛夫学院，佩雷尔曼成为黎曼空间和亚历山德罗夫空间几何（传统欧几里得几何的扩展）方面的专家，并开始在俄罗斯和美国领先的数学期刊上发表文章。1992年，佩雷尔曼受邀到纽约大学和石溪大学各学习一个学期。那年秋天，当他前往美国时，俄罗斯经济已崩溃。麻省理工学院的数学家丹·斯特罗克（Dan Stroock）回忆说，他那时曾将不少美元走私到俄国，送给斯特克洛夫研究所的一位退休数学家，这位数学家和他的许多同事一样，当时非常贫困。
可想而知，佩雷尔曼这时候很高兴能来到国际数学界之都美国。他每天都穿着同样的棕色灯芯绒夹克，并以面包、奶酪和牛奶为食来省钱。他喜欢步行到布鲁克林，在那里他有些亲戚，还可以买到传统的俄罗斯黑面包。他的一些同事被他几英寸长的指甲所惊讶。他说：“如果指甲要长，我为什么不让它们长呢？” 每周一次，他和一位名叫田刚的年轻中国数学家开车前往普林斯顿大学，参加在那里的高等研究院的研讨会。
几十年来，高等研究所和附近的普林斯顿大学一直是拓扑研究中心。七十年代末，普林斯顿大学数学家威廉瑟斯顿提出了一种对三维流形进行分类的分类法。他认为，虽然流形可以呈现出许多不同的形状，但它们都有一个“首选”的几何形状。
瑟斯顿提出，每个三维流形都可以分解为八种类型中的一种或多种，也包括球形类型。瑟斯顿的理论（后来被称为几何化猜想）描述了所有可能的三维流形，因此是对庞加莱猜想的有力概括。如果这一点得到证实，那么庞加莱猜想也将得到证实。
1982 年，瑟斯顿因其对拓扑学的贡献而获得了菲尔兹奖。那一年，康奈尔大学的数学家理查德·汉密尔顿发表了一篇关于“里奇流”方程的论文，他觉得该方程可能会解决瑟斯顿猜想以及庞加莱猜想。就像热方程描述热量如何在物质中均匀分布（例如，从金属板的较热部分流向较冷部分）以产生更均匀的温度一样，里奇流通过消除不规则性，提供了更均匀的几何形状。
汉密尔顿是辛辛那提一位医生的儿子，他打破了数学界对书呆子的刻板印象。他很不讲究，骑马、冲浪，交过很多女友。他虽然很聪明，但把数学视为生活的乐趣之一。所以虽然有这些开创性文章，但发表的文章相对较少，他的研究生也少。佩雷尔曼读过汉密尔顿的论文，并去听他在高等研究院的演讲。佩雷尔曼对他的工作很感兴趣，但因为性格不同，他只是害羞地跟汉密尔顿说话。
“我真的很想问他事情，”佩雷尔曼回忆道。“ 其实我不必害羞，汉密尔顿总是面带微笑，很有耐心。他实际上告诉了我一些几年后他才发表的东西，毫不吝啬。汉密尔顿的大方慷慨确实吸引了我。我不能说大多数数学家都是这样做的”。
“我当时正在做不同的事情，尽管偶尔我会考虑里奇流，”佩雷尔曼说道。“你不用是一位伟大的数学家就能看到这对几何化有用。我感觉我在这方面知道的不多，所以我一直在问他问题。”
1993年，他得到在伯克利为期两年的奖学金。在那里，汉密尔顿在校园里做了几次演讲，其中一次他提到他正在研究庞加莱方程。汉密尔顿的里奇流策略很有技术性，用起来不容易。在伯克利的一次演讲结束后，他也告诉佩雷尔曼他最大的障碍。当空间在里奇流下变得平滑时，某些区域会变形为数学家所说的“奇点”。一些被称为“颈部”的区域变成了无限密度的衰减区域。更令汉密尔顿烦恼的是一种他称之为“雪茄”的奇点。汉密尔顿担忧的是，如果雪茄形成，可能就不能实现均匀的几何形状。佩雷尔曼意识到，他自己的关于亚历山德罗夫空间的论文可能会帮助汉密尔顿解决雪茄问题，并进而证明瑟斯顿猜想和庞加莱猜想。“有一次，我问汉密尔顿，他是否知道我已经证明但未发表的某个结果，可能非常有用，”佩雷尔曼说。“但我发现他根本听不懂我在说什么。”
在伯克利分校的第一年结束时，佩雷尔曼已经写了几篇引人注目的原创论文。他被邀请在 1994 年 I.M.U 上发表演讲。在苏黎世举行的大会上，并受邀申请斯坦福大学、普林斯顿大学、高等研究院和特拉维夫大学的职位。和丘成桐一样，佩雷尔曼也是一位令人生畏的解决问题能手。他不是花费数年时间构建复杂的理论框架或定义新的研究领域，而是专注于获得特定的结果。
佩雷尔曼喜欢同时解几个问题。但在伯克利，他发现自己一次又一次地回到汉密尔顿的里奇流方程以及汉密尔顿认为他可以用它解决的问题。佩雷尔曼的一些朋友注意到他变得越来越宅和远离生活。来自圣彼得堡的客人住在他的公寓后，对他有的陈设如此简陋感到震惊。当斯坦福大学招聘委员会的成员向他索要简历时，佩雷尔曼拒绝了这个请求。“如果他们了解我的工作，就不需要我的简历，”他说。“如果他们需要我的简历，他们并不了解我的工作。”
最终，他收到了几份工作机会，但他全都拒绝了，并在 1995 年夏天回到圣彼得堡，继续他在斯特克洛夫研究所原来的工作，在那里他的月薪不到一百美元。 但他告诉一位朋友，他在美国存了足够的钱来度过余生。他的父亲两年前搬到了以色列，他的妹妹计划大学毕业后去以色列和他一起生活，只有他的母亲决定留在圣彼得堡，佩雷尔曼就搬去和她一起住。“我意识到在俄罗斯我工作得更好，”他说。
年仅二十九岁，佩雷尔曼已经确立了数学家的地位，但基本上没有专业责任的负担。他可以自由地研究他想要解决的任何问题。斯坦福大学数学家雅科夫·埃利亚什伯格（Yakov Eliashberg）在伯克利认识佩雷尔曼，他认为佩雷尔曼回到俄罗斯就是为了研究庞加莱方程。“为什么不呢？”佩雷尔曼说道。
1995 年，汉密尔顿发表了一篇论文，讨论了他完成庞加莱证明的一些想法。读完这篇论文后，佩雷尔曼意识到汉密尔顿在克服他提到的障碍（前面提到的脖子和雪茄）方面没有任何进展。然而，佩雷尔曼认为他找到了解决的方法。1996年，他给汉密尔顿写了一封长信，概述了他的想法，希望能够合作。“他没有回答我，”佩雷尔曼说。“所以我决定独自工作。”
2002 年 11 月 12 日，丘成桐收到了一封来自一位俄罗斯数学家的电子邮件，他没有马上想起这个数学家是谁。“我想提请您注意我的论文，”电子邮件中写道。
前一天，也就是11 月 11 日，佩雷尔曼在 arXiv.org 上发表了一篇长达 39 页的论文，题为“里奇流的熵公式及其几何应用”，该网站是数学家用来发布预印本的网站，这些文章等待在审稿期刊上发表。然后，他通过电子邮件将论文摘要发送给美国的十几位数学家，其中包括汉密尔顿、田刚和丘成桐，这些人多年来都没有收到他的消息，现在，在邮件的摘要中，他解释说他写了几何化猜想的“证明草图”。
我把故事就讲到这里了，其它后面的事情种种有必要再说。
总之，佩雷尔曼逐渐把他的证明全部发上来了。