本文由加州大学伯克利分校统计系和谷歌 DeepMind 的团队联合发表,研究了预训练后的 Transformer 的基于上下文学习 (In-Context Learning) 的能力。他们用简洁的数学理论证明了:Transformer 可以基于上下文学习到一种类似最小二乘的算法,这种学到的算法在新的数据集上能学到正确的线性模型。

论文地址:https://arxiv.org/pdf/2306.09927.pdf
基于上下文学习 (ICL,In-Context Learning) 是大语言模型的特殊能力。它通常指的是:一个经过预训练的语言模型,当你输入一些具体的任务指示和少数几个范例 (demonstration) 之后,再输入一个新问题 (query input),该模型可以依据提供的范例给出正确的解答或者标注 (label)。注意,在进行基于上下文的学习的时候,原先经过预训练的模型是不需要经过任何微调 (fine-tuning) 的。也就是说,原模型的参数完全不会变化。这大大节省了微调所需要的数据。举个例子,假设你需要 GPT 做翻译任务,你提供了一些范例:狗 ——dog;猫 ——cat。然后你想知道「人」怎么翻译。这个时候你不需要对模型进行任何微调(尽管训练的时候并没有使用翻译的数据集),你只需要输入:请将中文翻译成英文。例如:狗 ——dog;猫 ——cat;人 ——?
GPT 可以给出你正确的回答(不信你可以自己试试)。在 GPT3 及此后的许多大模型中,人们都观察到了 ICL 的现象 [1]。如何理解这种现象,目前学术界并没有给出统一的答案。一种观点认为,GPT 可以从提供的范例中学到某些算法,然后再将这些算法用到新的问题中。例如,从「狗 ——dog;猫 ——cat」中,GPT 也许学到了一种「可以用于文本翻译」的算法,然后在将这种算法用在新的问题「人 ——?」中。至于学到了什么算法,不同机构通过实验得出了一些结论 [2,3,4]。下表中,我们使用约等号,表示并没有严格的理论说明 GPT(或者类似结构)严格学到了这个算法,但是它和该算法在任务上的表现几乎一致。
本文首次从理论上证明,经过预训练的 Transformer 在线性回归模型上学到了与最小二乘十分类似的算法,它们都能基于上下文学到正确的线性模型。本文考虑的是一个简化的线性 Transformer 模型,所有的数据来源于无噪音的线性模型。我们考虑这样一个序列到序列 (sequence-to-sequence) 的函数:我们用一系列的数据和标签 (x_i,y_i), i=1,2,...,N, 来模拟一个任务中的范例。想象所有的 x_i 就是中文词语,对应的 y_i 是对应的英文翻译。我们还有一个需要给出预测的输入 x_query(想象我们有一个中文单词需要翻译),对这个输入,它对应的输出是 y_query,我们希望模型准确的预测它。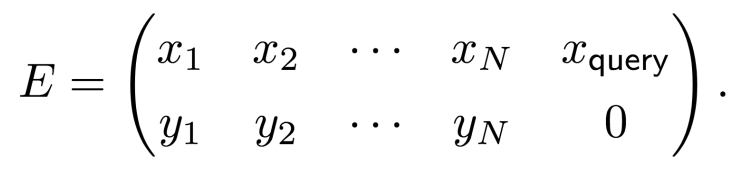
这里我们没有将 y_query 放进去,是因为这个矩阵会被输入给 Transformer,而我们希望得到的预测是 y_query。我们将这个数据编码矩阵 (embedding matrix) 输入到如下的单层线性 Transformer 中: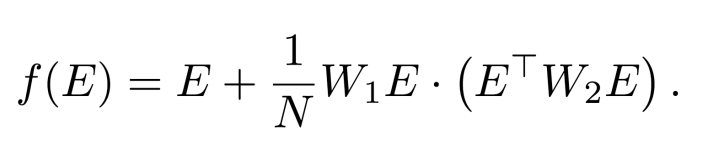
是的你没有看错,这就是一个(一层的、线性的)Transformer。这里的输入和输出是同样大小的矩阵,第一个加数 E 表示经典的残差连接,后面的 W_1 表示 value 矩阵,而 W_2 则是把 key 和 query 矩阵的乘积直接当成了一个矩阵。之所以称其为「线性的」Transformer,是因为我们去掉了经典 Transformer 中的归一化(除以某个系数后加上 softmax)和非线性激活函数,将其替代为直接除以 token 矩阵 E 的大小(乘以 1/N)。我们将输出矩阵的右下角元素记为ŷ_query,它是模型对 y_query 的预测。我们假设所有的数据来自于一个随机的线性模型,即对于 i=1,2,...,N,有 y_i = w・x_i 以及 y_query = w・x_query。我们假设 w 服从标准高斯分布,而 x_i 独立同分布地服从一个均值为 0,方差为 𝝠 的高斯分布。在训练的过程中,我们最小化如下的目标函数: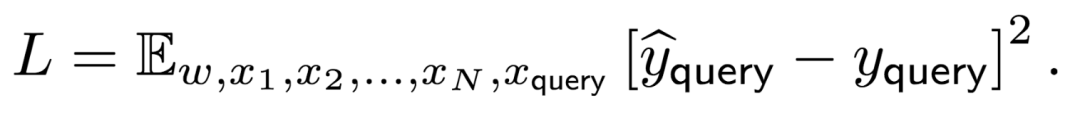
本文从理论上证明了,当我们用 gradient flow(也就是 gradient descent 加上无限小的步长)对上述的目标函数进行优化的时候,参数矩阵 $W_1$ 和 $W_2$ 都能收敛到某个特殊的全局最优解。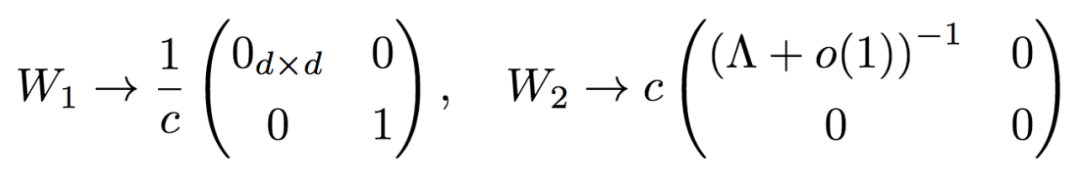
更重要的是,假设我们模型中的参数已经收敛到这个全局最优解,而此时我们有一个新的任务(新的 weight 向量 w)和一系列针对这个任务的范例(新的 x_i , y_i 和 x_query),当我们把这些数据堆成一个同样格式的 embedding 矩阵 E 然后输入给训练好的模型时,这个模型会给出什么样的预测呢?通过简单的计算(真的很简单)可以得到,模型的预测是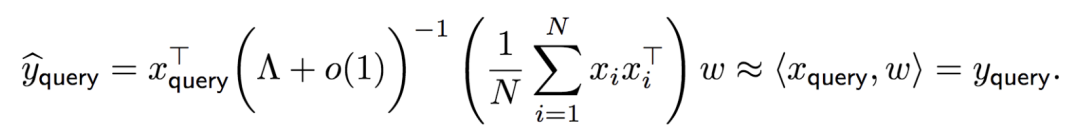
为什么会有这个约等号呢?是因为假设我们的范例足够多(N 足够大),大数定律告诉我们中间括号里的 empirical covariance matrix 会几乎处处收敛到真正的 population covariance matrix,而我们如果进一步忽略前一个括号中的 o (1) 小量,就可以将 𝝠 和它的逆抵消。从而,模型的预测近似地等于 w・x_query 也就是真实的,我们所希望预测到的数据标签 y_query。也就是说,当提供的范例足够多的时候,经过预训练的一层 Transformer 可以从范例中学到正确的线性模型对应的参数,并将这个参数应用到新的输入中,得到正确的标签预测。本文还研究了更多关于 Transformer 的 ICL 能力的有趣现象。点击「阅读全文」获取原文信息。- 非线性任务?—— 当我们提供的范例来自一个非线性任务时,经过预训练的 Transformer 学到了对应的最佳线性预测。这个结论可以被泛化到更一般的联合分布的情况。
- 分布转移 (distribution shift)?—— 前人的实验中观察到,当测试时的任务分布或者数据分布不同于训练时的分布时,Transformer 能够承受一些种类的分布转移,但在另一些分布转移中会表现的很差。本文从理论上研究了 Transformer 面对分布转移时的行为,并成功解释了来自斯坦福的论文 [2] 中关于分布转移的大部分实验现象。
- 收敛速率?—— 本文将基于上下文学习的能力解释为一种学习新算法(新函数)的能力,并给出了对于训练范例的数量和测试范例的数量二者的收敛速率。值得注意的是,线性 Transformer 对于二者的收敛速率是不同的。
- 随机协方差矩阵?—— 本文还证明,如果数据来源的协方差矩阵是随机的,一层的线性 Transformer 无法从上下文中学到正确的线性模型。我们的实验结果表明,更复杂的模型(诸如 GPT2)依然不能完全解决随机协方差矩阵的问题。
- 基于上下文学习的理论框架?—— 本文建立了严格的基于上下文学习的理论框架,区分了基于上下文的训练 (In-Context Training) 和基于上下文的学习能力 (In-Context Learnability) 这两个概念。
[1] Tom Brown et al. “Language models are few-shot learners”. In: Advances in neural information processing systems 33 (2020), pp. 1877–1901. https://arxiv.org/abs/2005.14165. [2] Shivam Garg et al. “What can transformers learn in-context? a case study of simple function classes”. In: Advances in Neural Information Processing Systems 35 (2022), pp. 30583–30598. https://arxiv.org/abs/2208.01066 [3] Ekin Akyürek et al. “What learning algorithm is in-context learning? investigations with linear models”. In:arXiv preprint arXiv:2211.15661 (2022). https://arxiv.org/abs/2211.15661 [4] Kabir Ahuja, Madhur Panwar, and Navin Goyal. “In-Context Learning through the Bayesian Prism”. In: arXiv preprint arXiv:2306.04891 (2023). https://arxiv.org/abs/2306.04891

© THE END
转载请联系本公众号获得授权
投稿或寻求报道:[email protected]