说说把我吸引到华尔街的那个公式

一

我对科学感兴趣，但对人文学科同样感兴趣。只是在我上大学的时候，人们对人文科学不太重视，或者说不太尊重，因此除了文学我对人文学科没有太多了解，就这样我选择了当时最受人仰视的近代物理，连一般物理都不行。两年后，我对人文科学有了更多了解，尤其是需要数理基础的人文科学，那就是经济学和管理科学了。我上的那所大学没有人文学科，刚刚成立的一个科目就是系统工程，算是一种管理科学，于是我就转到那里了。研究生期间我想转到经济，特别与北大经济学厉教授的学生们建立了关系，想在硕士毕业之后去那里读博士。但是天有不测风云，各种事发生了之后综合考虑了一下，转念去留学了。

到了美国，觉得是“他人”的国度，就不要再搞经济了。想学完了到某个学校教教书就心满意足了。但是渐渐的，得知华尔街需要我们这种人，这让我的心又动了起来。华尔街毕竟跟经济有关，准备一下吧。问询了熟悉情况的同学，知道华尔街需要的主要就是懂一个特殊的数学公式的人，当然，懂这个数学公式也需要多年的数理教育，否则不可能懂，并且也能对那个公式进行计算，当然也要有计算机知识。我准备了一下，经过两个公司的面试，后来就去华尔街工作了。

那个公式叫做布莱克-舒尔斯公式，是给期权定价的公式。期权是建立在我们熟知的股票或债券基础上的证券，是一种权利，比如说，一个股票的看涨期权就是在某个时间以某个预定价钱买那个股票的权利。如果在那个时间，股票的价格超过那个预定的价格，就买，这个叫行权。如果股票的价格低于预定价格，就不行权。行权得到的利润超过买这个期权的价格就赚钱，其它情况就亏了。期权的种类很多，除了看涨，还可以看跌。这些期权的价格应该是多少，就是布莱克-舒尔斯公式能提供帮助的。发现这个公式的两个美国人之一迈伦·舒尔斯和另一个也独立发现它的罗伯特·C·墨顿在1997年获得诺贝尔奖，而另一位发现者费希尔·布莱克因为已经去世所以没有得到。1997年是我在华尔街上班的第二年，对这个消息当然也是很激动，也说明当时期权在市场上的火热程度。

期权一直火热到2008年的金融危机，以后也不是不重要，但它的风险很大，政府和银行对它的监管力度越来越大，就没有之前那么火热了。

但是，这是我人生中很重要的一部分呢。

想起这个事，是因为今天翻我的一堆书时，正好看见好多年未读的布莱克传记，于是想把这个公式的发现按照书中的描述给我的读者写写，换句话说，就是布莱克、舒尔斯和墨顿是如何推导出这个公式的故事。

二

1968年夏天，罗伯特·C·默顿年仅24 岁，是麻省理工学院的研究生。和我在美国学的差不多，应用数学。和我不同的一个方面是，他老爹是哥伦比亚大学著名社会学家罗伯特·K·默顿。这不是一个很小的不同，因为这让他能够和著名的经济学家保罗·萨缪尔森（Paul Samuelson）很熟，并成为他的帮手。萨缪尔森很快就成为第一位获得诺贝尔经济学奖的美国人。

那天，他们在麻省理工学院萨缪尔森的办公室里谈到了期权。谈话的起因是 1967年爱德华·索普 (Edward Thorp) 和辛·卡苏夫 (Sheen Kassouf) 的一本书，叫《打败市场：一个科学的股票市场系统》。书里提到一种更科学的方法，通过购买股票并同时卖空同一股票的“认股权证”来在股票市场上赚钱。认股权证和我上面说的期权差不多，是公司发行的一种股票期权，让持有人有在未来指定日期之前的任何时间以指定价格购买公司股票的权利。 1968年，还没有在期权市场上的期权交易，但能交易的认股权证有一百多个。索普和卡苏夫声称他们找到了一种方法能识别被高估的认股权证，并通过同时做相应股票的进行来进行套利获利。套利这个词非常重要，一般指的是买一个卖一个没有太大风险就能赚钱。我这一代和之前的中国人可能熟悉一个词叫投机倒把，差不多，比如从便宜的地方买点什么，拿到贵的地方卖。那时候我们认为是犯罪，但其实不就是把东西从不太需要的地方拿到更被需要的地方为人民服务吗？更正式一点，套利的作用是让市场更有效，把偏离市场的价格拉回来，因为价格太低的价格套利者来买就会把它拉上来。太贵的价格被套利者卖出去会把它拉下来。

萨缪尔森之所以对这本书感兴趣，是因为他也一直在想如何为认股权证定价的问题，还在 1965 年麻省理工学院期刊《工业管理评论》上发表了尝试的解决方案。在那篇文章中，他和麻省理工学院数学教授亨利·麦基恩一起推出了一个定价方程，假设条件是：公司股票及其相关认股权证的预期回报都是已知的，并且在认股权证的整个生命周期中都是恒定的。他使用 a 代表股票的预期回报，ß 代表认股权证的预期回报，所以那个模型被称为萨缪尔森的 alpha -beta 模型。根据 a 我们可以知道股票的预测价值，那么我们可以在期权终止日期对认股权证进行估值，因为认股权证那天的价值依赖于股票的回报，然后再使用假定的认股权证回报将那个估值折现到现值。问题是我们不知道股票的预期回报，而且无论如何这些回报都不太可能随着时间的推移保持不变。 

1968年，卡苏夫指出萨缪尔森1965 年模型的局限性。萨缪尔森觉得有必要做出回应，但似乎需要更复杂的数学方法。而默顿有很好的数学背景，正好是萨缪尔森所需，而且默顿还有丰富的交易认股权证的经验，所以他很感兴趣和萨缪尔森一起来做个研究。很快他们得到了一些结果，共同撰写了一篇论文，叫做“效用最大化的认股权证定价的完整模型”，并准备将其发表在《工业管理评论》上。这次，他们没有将 a 和 ß 设置为外生参数，也就是说不是假设它们已知，也不是恒定不变的。相反，这次他们提出了一个经济学里常用的均衡模型，这两个量都在考虑到投资者的风险偏好，在每个时期按供求关系被决定。现在看起来，他们对这个问题的理解还不够充分，只是采用了数学方法建立一个模型，并没有看到后来布莱克-舒尔茨-默顿公式所提供的对期权及金融市场的洞见。

所以，他们以为这就可以结束了。 1968 年 10 月，麻省理工学院-哈佛数学经济学联合研讨会要开始了。这是一场盛大的活动，在哈佛大学霍利奥克中心举行，萨缪尔森的名望使他成为会议宣传的招牌。哈佛大名鼎鼎的人物——肯尼思·阿罗（Kenneth Arrow）、瓦西里·莱昂蒂特（Wassily Leontiet）、兹维·格里利切斯（Zvi Griliches）、罗伯特·多尔菲曼（Robert Dorfiman）、亨德里克·胡撒克（Hendrik Houthakker）——还有来自其他地区大学的重要教授也会来访。这个活动是不允许学生参加的，但是萨缪尔森安排了罗伯特·默顿参加，不仅如此，萨缪尔森本来是要做一个学术演讲的，但他安排·默顿代替他发表演讲。这说明他对默顿在工作中的满意和愿意栽培他的用意。不过在我看来，虽然不大可能他对这篇文章不重视，但还是没有足够的重视。原因是他们还没有对期权的定价找到答案，也不知道答案的意义所在。反过来因此他们也没有再做进一步的研究。

当演讲的时刻到来时，萨缪尔森站起来讲话。 “这是一篇联合论文，我的合著者将给大家介绍它的内容。我想称他为教授，但他不是教授。我想介绍他为博士，但他还没有博士学位。所以我现在将他介绍为罗伯特·默顿先生。”这个事情可以总结为：默顿与保罗·萨缪尔森联合发表了一篇关于认股权证定价看似深奥话题的论文，年轻的默顿引起了数理经济学精英的注意。

事情就这样结束了。对于默顿来说，权证定价的研究工作让他得到了南加州一家银行的咨询工作，但仅此而已。在默顿后来为诺贝尔委员会撰写的自传中，他回忆起那段咨询工作说：“具有讽刺意味的是，我在那里工作时为他们开发了“等西格玛风险等收益”的模型，如果我把这个模型推广到连续交易的极限情况，就会导出布莱克-斯科尔斯定价公式。”但他还没有想到这样做。他与萨缪尔森一起完成了一个权证论文，他并不知道这个工作的意义，现在他要把研究精力集中在他认为更大、更重要的问题上，即不确定性下的跨期选择，这项工作将成为他博士论文的重点。 

默顿在这个工作里开始展现他的数学能力，这也是他后来以不同方式导出布莱克-舒尔茨公式的原因。他用连续时间的随机过程数学来解决这个问题，是第一位这样做的经济学家。在这样的连续时间分析框架中，随机因素在每个时刻都在起作用，就好像在每个无限小的时刻，都有一个决定资产回报的骰子被重新扔到桌面上滚动，因此任何有限时间间隔内的回报，无论多短，都是很多这样随机变化加起来的和。

他工作很快，就在那次会议的下个月，即 1968 年 11 月，默顿在麻省理工学院的一次研讨会上发表了他博士论文的第一部分，这篇论文随后以“不确定性条件下的长期（终身）资产组合选择：连续时间案例” 为题发表在哈佛的经济与统计评论杂志上。这是一个需要同行审阅的杂志，所以在默顿的心中，这个才是重要的东西，而不是权证定价。

三

在波士顿一家管理咨询公司工作的费舍尔·布莱克不知何故听说了默顿的研讨会并去听了。会议结束后，他走向默顿说，“如果你有兴趣的话，我有一篇关于这个主题的论文。”他指的是他那篇 1968 年 11 月 1 日修订版第 6B 号财务报告杂志上的《投资的时间多元化》。这是他们两人第一次见面，谈的却不是他们后来一起留名的工作。两人也没有产生很大火花。随着时间的推移，两个人开始在不少研究问题上互动，但当时他们的风格截然不同。

1967 年春天，布莱克曾去见萨缪尔森，为共同基金听证会做准备，但两人并不合拍。布莱克给萨缪尔森的印象是衣着过度，甚至拘谨，在这方面让萨缪尔森想起了哈佛物理学家朱利安施温格。更糟糕的是，萨缪尔森认为布莱克的想法大都源于自由意志主义（libertarianism）思维模式，倾向于认为政府无权干涉私人合同。 

布莱克在麻省理工学院另一位著名教授弗朗哥莫迪利亚尼那里运气要比在萨缪尔森这里好，莫迪利亚尼有个著名的周二晚上金融研讨会，布莱克作为嘉宾经常出席。

默顿作为受过经济学训练的人，很自然地会将终身投资组合选择问题视为动态规划问题。要理解动态规划，你可以想象一个人展望他的未来一生，对每个阶段消费多少、收入和储蓄多少做出预期，并决定承担多少风险。评估所有不同的可能时会考虑到他的时间偏好和对风险的态度，并做出能够最大限度地获得“效用”的选择。这是经济学家的自然方法。

然而，布莱克不是经济学家，他与一些非学术机构的人一起研究发展了一个叫做资本资产定价模型（CAPM）的现代金融学模型，那是他精通的东西，所以他采取的策略不同，他是将这样的问题视为分散化的问题。 “正如一个投资者在跨多种不同证券的投资上所做的，为了最大限度地减少与时间相关的风险，他应该将投资分散到不同的时间间隔，以最大限度地减少风险。”

我们知道，资本资产定价模型将每只股票视为一个骰子，它要求在所有骰子上的分散化。布莱克的想法是将每个时间段的市场投资组合视为一个骰子。那么，终生投资组合就是决定分配多少财富来解决个人一生中不同阶段将遇到的骰子的问题。分散化原则可以立即给出答案，个人应该在每个骰子上下完全相同的金额，逻辑很简单，但是，如果你在年轻时承担更多风险，然后在年老时少承担风险，就像许多人建议的那样，那么你增加了风险，但不能使预期回报最大化，因为你投资的时候，可能会遇到一连串糟糕的骰子。正如将财富分散在许多不同的风险股票上而不是在单一股票上一样，将财富分散在许多不同的风险时间段上也比集中在特定时刻增加风险更好。如果每个时间段的风险都相同，那么你可能应该在年轻时和年老时承受完全相同的风险。今天和明天“相同金额”是指明天的金额与今天投资的金额具有相同的价值。假设利率是 r，我们可以按照这个利率将今天的钱变成明天的钱，那么今天的 1 美元与明天的 $(1 + r) 是一样的，时间分散化原则是说，如果我们计划今天投资 $x，我们应该计划明天投资 $( 1+r)x。在现实世界中，由于不确定性，事情并不那么简单，但基本逻辑适用。

正确与否，我们这里不说，但可以看到，布莱克习惯用直觉。

人们不知道布莱克是怎么开始对认股权证（期权）定价问题感兴趣的，也许他可能听说过萨缪尔森-默顿的论文。不论怎样，他对此做了研究，在 1969 年 6 月就获得了期权定价问题的关键性微分方程。他得到这个方程，却不知怎么来解它。换个好的物理学家，就会知道这个方程是物理学家熟悉的热交换方程的形式，并有已知的解法。如果默顿见了这个方程，也一定会知道如何解这个方程。但默顿不知道。布莱克虽然无法解这个问题，但他从方程上看出，如果他的方程正确，那么萨缪尔森-默顿的公式就有问题。他们的公式与股票和认股权证的预期回报相关，可这两者都没有出现在布莱克的方程中。

我想，也许布莱克也对自己这个方程不是那么有信心，或者，他还是不知道这个问题的重要性。否则，他一定会把它解出来，发表，并指出萨缪尔森-默顿方法的错误。那样的话，如果诺贝尔奖在他生前发给他的话，就没有其他人的事了。但是他没有，他把这个方程放进了抽屉里，等待着下一个时机。

另一方面，萨缪尔森和默顿这些来自经济学领域的人，很自然地要从个人投资者的角度思考期权定价问题，考虑期权到期时可能的价值和概率，然后把那些未来价值贴现到现在。从这个角度来看，期权的现在价格就必然取决于投资者对风险的态度。更重要的是，他们会这样想，由于期权比股票风险更大，如果投资者同时持有期权和股票，则期权的预期回报必须高于股票的预期回报。高多少必须取决于投资者对风险的态度和期权的风险性。但是，期权的风险性随着股票价格的变化而变化，这就让这个问题看起来很复杂。但这也预示着在其中有什么有趣的事。 

相比之下，根据CAPM ，布莱克很自然地认为期权定价问题本质上是计算它在每一时刻市场风险敞口的问题。这样，更自然的是方法是写下一个微分方程来描述期权的价值如何随时间变化。布莱克的这种 CAPM 解决方法出现在后来 1973 年发表的布莱克-舒尔茨（ Black-Scholes）文章中，标题中有“另一种推导”的字句，这个“另一种推导”实际上是他解开这个问题的钥匙。 1969 年那个时候，布莱克不仅将 CAPM 的解法用于期权，还用于终身投资策略、货币和商业周期。

他和当时的人一样，关心的是认股权证，不过，它与期权极为相似，所以这里我们就直接谈期权定价。他是这样解决这个问题的，首先他假设期权价格 V 的公式是股票价格 S 和时间 t 的函数，即 V(S, t)。因为期权价格取决于股票价格，股票价格的小幅波动就会引起期权价格的小幅波动，也就是说V的变化ΔV= V1(S ,t)ΔS。V1(S ,t)是对第一个变量S的偏导数。在CAPM理论中，每种证券的市场风险都可以用一个所谓的贝塔值衡量，贝塔描述这个证券与有代表性的市场指数之间的统计相关关系。期权的市场风险也是通过其贝塔值衡量，但由于ΔV= V1(S ,t)ΔS，它与股票的市场风险之间就应该存在类似比例的关系。根据这样的思路，布莱克先用贝塔值得到了期权和股票的预期回报方程。然后像做泰勒级数展开把样把期权回报表示成一些基本的项，再进行一些简单代数运作，就得到了关键的微分方程。

在这个方程里，其中 r 是利率， 是股票收益的方差。尽管布莱克最初不知道怎么解这个方程，但他这个方程包含了期权定价的秘密，足以让他比萨缪尔森和默顿知道的要多。布莱克以他典型的简洁方式评论道：“ 认股权证的价值并不取决于股票的预期回报，也不取决于任何其他资产的预期回报。我发现这很重要。” 经过很多天尝试解这个方程不果之后，布莱克把这个问题放到了一边。他关心的是如何应用 CAPM，而且还有很多想法，所以他就继续研究那些想法去了。布莱克和默顿一样，觉得认股权证的估值问题不那么重要。他们觉得这个研究不过是象牙塔里的一时好奇心，对一些人来说也许重要，但对更广泛的世界来说不重要。除了那些被可能的巨大价格波动所吸引的投机者之外，谁会关心权证估值？当然不是布莱克了。于是他把方程式放在抽屉里，开始研究其他事情。

四

1969 年秋初的一天，在布莱克的办公室里，他和麻省理工学院教授迈伦·斯科尔斯讨论关于富国银行的咨询工作。谈话中舒尔斯开启了期权定价的话题。在麻省理工学院，他在指导一名硕士生，这个学生有一些期权价格的数据，他想在论文中分析这些数据。舒尔斯一直在阅读有关这个问题的最新研究成果。他一直在思考如何构建一个投资组合，其中包括期权和它的标的股票，并达到零贝塔对冲（也就是没有系统性风险，系统性风险指的是和市场指数一样的风险），然后把 CAPM 应用于这个组合以解决期权定价问题。

当舒尔斯说这些话的时候，布莱克从他的档案中抽出一张纸，上面有他推导出的微分方程。于是他们开始共同研究这个期权定价问题。舒尔斯提出了几种他的解决方法。布莱克的方法是寻找一个期权价格，“它应该是多少”，而舒尔斯是从投机套利的角度来看这个问题。由于期权的价值随着标的股票的价值而变化，因此可以想象地建一个对冲组合，做多期权并做空股票。如果能正确地进行对冲，这样的组合头寸就没有市场风险。舒尔斯说，这不会是完全无风险的，但他认为剩余的风险是可以分散掉的，因此不用定价。那么，根据 CAPM，整个头寸的预期回报率应等于无风险利率，并且由于股票的价格已知，因此应该能够通过这些关系找出期权的价格。问题就是如何确定合适的对冲比率。

但舒尔斯所需的对冲比率当然就是布莱克公式ΔV= V1(S ,t)ΔS 里面的一阶导数V1(S ,t) 。一个含有多头期权和V1(S ,t)空头股票的头寸应该有等于无风险利率的预期回报。当根据期权和股票的预期收益计算该对冲投资组合的预期收益，并展开ΔV 的表达式时，一些简单的代数运作直接就可以导出布莱克那个关键微分方程。因此，舒尔斯的风险套利方法是理解布莱克的那个方程成立的另一种直观方式，因此证实了布莱克的方法是走在正确的道路上的。但他们俩还是不知道怎么解这个方程。舒尔斯似乎并不比布莱克数学更好。然而，他们一起努力，竟以一种最不可能的方式解决了这个问题。怎么解决的呢？

舒尔斯知道凯斯·斯普伦克尔（Case Sprenkle），耶鲁大学的一名研究生，提出了一个不完整的期权价格公式。斯普伦克尔用的方法是数据分析，所以不能给出意义，但似乎和市场价格相近。看着这个原始公式，布莱克和斯科尔斯开始考虑公式中必须缺少什么，而不是必须包含什么，从而实现了关键突破。 

按照 CAPM 类似的分析，布莱克和斯科尔斯都觉得这个公式应该是期权市场风险的函数，期权市场风险大概是标的股票市场风险的几倍，但是标的股票的预期回报率并没有出现在该股票中。这就是为什么，根据斯科尔斯的说法，“我们都对这个微分方程感到惊讶”。

在这个微分方程的推导中，股票的市场风险和期权的市场风险完全相互抵消了。既然如此，他们俩考虑将斯普伦克尔的公式应用于市场风险为零的特殊情况，这给他们提供了导出正确解的机会。 

斯普伦克尔的期权价格公式要求用户提供两个输入：股票的预期回报以及评估期权收益的贴现率。但布莱克和斯科尔斯从他们的微分方程中知道，股票的预期回报不能出现在正确的公式当中。他们就想，他们可以假设他们考虑的期权是基于一个零贝塔股票上的，这意味着他们可以将股票的预期利率设置为无风险利率。此外，由于零贝塔股票的期权也将具有零贝塔，因此他们可以使用相同的利率作为适当的贴现率。将这些利率代入斯普伦克尔的公式，他们得到了零贝塔股票期权价值的公式。但这个公式也满足他们的微分方程，这意味着它也是期权价格的一般公式。他们的关键微分方程就这样被解开了。 

布莱克-舒尔斯看涨期权的定价公式为： 

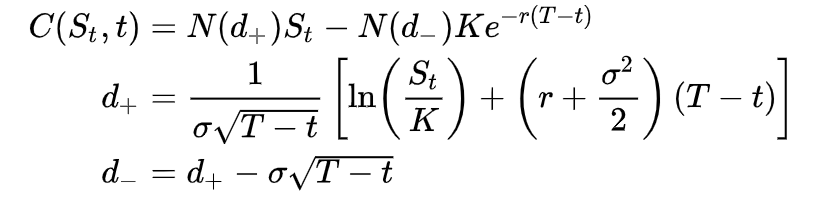
N(d) 是描述股票价格分布的累积正态密度函数，K为行权价格，T为到期日期，t 是当前日期。从这个公式很容易计算出正确的对冲比率就是：

解决了定价问题后，布莱克和斯科尔斯转向应用问题。谁应该关心他们的公式？投机者当然会关心，这将使他们在与其他投机者的竞争中具有优势，但经济学家关心的是一般社会福利问题，期权定价会有帮助吗？一个自然的应用是公司证券估值问题。早在 1958 年，莫迪利亚尼和米勒就表明，公司的总价值不受其融资方式的影响，无论是完全通过股票、完全通过债务，还是两者的混合。他们没有回答的问题是，股票价值和债务价值如何受到公司融资方式的影响。布莱克可能从他与一些经济学家的谈话中意识到了这个问题，而舒尔斯则从他与默顿·米勒的谈话中意识到这个问题。期权公式似乎可以提供答案。

从期权定价的角度来看，公司债券持有人可以被视为公司资产的所有者，他们发行了看涨期权（股票）给股东，其行权价格就是债券的面值。这是因为，在未来任何时候，当公司清算时，债券持有人将首先获得债券面值的报酬，只要公司价值超过面值。股票持有人将获得剩余的一切。因此，布莱克-斯科尔斯公式可用于对股票进行估值，而债券的价值则作为公司总价值的剩余价值。这个计算值与债券面值之间的差异提供了由于违约可能性而产生的折扣的一个衡量标准。这样，布莱克-斯科尔斯对期权定价问题的解决方案似乎为公司金融中传统的估值问题开辟了一种新的“风险债权估值”方法。

在 1970 年 7 月 27 日至 29 日由舒尔斯在麻省理工学院组织的第二届富国银行资本市场理论会议上，布莱克和舒尔斯介绍了他们的公式以及对证券估值的应用。他们这次讲话的内容最早包含在他们的论文，“期权、认股权证和其他证券的理论估值公式”，日期为 1970 年 8 月。这篇论文最后说：“罗伯特·C·默顿（Robert C. Merton）有与我们相同的公式，在某种程度上开始于不同的假设。知道他的公式与我们的一致，这让我们更有信心地说我们在此过程中没有犯实质性错误。” 

五

舒尔斯第一次见到默顿是在 1970 年 2 月或 3 月，当时默顿在面试斯隆商学院的一个职位，随后他们开始定期互动，但不是关于认股权证的问题。正如斯科尔斯讲述的那样，“我想我们没有意识到我们都对这个问题感兴趣“。

在1970年七月的一个会议上，默顿第一次了解到了布莱克-舒尔斯公式。实际上，就是在布莱克和舒尔斯宣读论文的同一天的下午会议上，默顿也宣读了自己的论文，题为“资产市场的动态一般均衡模型及其在资本结构定价中的应用”。”在那篇论文中，默顿显然掌握了期权定价的或有债权估值应用的基本内容，但还没有提出正确的期权公式。

事实上，由于他错过了布莱克和斯科尔斯宣读论文的那场会，所以会议结束后他向舒尔斯询问此事。斯科尔斯解释了他们公式的推导，但默顿不相信结果的一般性。对他来说，问题出在 CAPM，因为默顿觉得CAPM 是一种非常特殊的资产定价理论，仅限于具有均值方差效用的一阶段静态问题。所以，基于 CAPM 的解决结果充其量可能是大致正确的，至少与他从他自己的更一般的跨期 CAPM 中得出的结果相比是这样。从这个角度来看，他自然对布莱克-舒尔斯提出的期权定价公式的普遍性持怀疑态度。布莱克和舒尔斯之所以取得这样的成就，仅仅是因为他们的推导基于 CAPM。 

他对布莱克最初对方程的推导持怀疑态度，因为它在使用贝塔来计算期权的预期回报时明确依赖于 CAPM。但他也对斯科尔斯偏爱的风险套利推导持怀疑态度，因为它依赖 CAPM 来论证零贝塔风险敞口应具有等于无风险利率的预期回报。所有这些依赖CAPM的假设都未必成立。默顿的跨期 CAPM 最重要的结果之一是“与经典的资本资产定价模型相反，风险资产的预期回报率，即使它们没有系统性或市场风险，也可能与无风险利率不同。”既然布莱克-舒尔斯公式依赖于 CAPM 的简化，这意味着可能还有更通用的公式有待找到。默顿决心找到它。 

当布莱克听说舒尔斯与默顿的谈话时，他很不高兴。他立即开始与斯科尔斯一起思考一种更通用的方法来解决这个问题，该方法将建立在风险对冲论点，但不依赖 CAPM。这个论点在会议后撰写的 1970 年 8 月草案中得到了体现。但这个论点也不能让默顿满意。为什么会期望对冲期权头寸的剩余风险是可分散的呢？

与此同时，默顿正在用自己的方式思考这个问题。对布莱克-舒尔斯风险对冲的思考，让默顿意识到，在他的连续交易框架中，可以通过在买标的股票中并结合借款来精确复制期权的回报模式，前提是可以在期权整个生命周期中的每个时刻都无成本地调整这个头寸。当然，在现实世界中瞬时无成本的投资组合调整是不可能的，但在连续时间数学框架中这完全可能，它具有至关重要的分析意义。由于可以通过价格已知的证券的动态交易来准确地复制期权的回报，因此可以在任何时刻准确地计算期权的价格，期权的价格就是复制投资组合的价格。 

要构建复制投资组合，需要知道每个时刻的对冲比率。那么，看涨期权只不过是，V1股价格为 S 的股票加上借入的 V1S-V。这一推理过程立即将默顿引向关键的微分方程，进而引向布莱克-斯科尔斯公式。 1970 年 8 月的一个星期六，默顿给斯科尔斯打电话：“你是对的。”默顿的推理线路被称为无套利方法，因为如果期权价格不完全等于复制投资组合的价格，那么通过购买期权和出售复制投资组合将获得套利利润，反之亦然。当然，这种说法仅在模型框架内严格正确，在实际交易环境中只能近似正确。因此，像布莱克和舒尔斯一样，默顿提出了理性期权定价的规范理论，因为他的理论告诉我们期权价格应该是多少，而不是根据套利者的行为必然是什么。然而，与布莱克和舒尔斯不同，默顿的推导根本不依赖于 CAPM 或任何其他资产定价理论。此外，默顿通过考虑可以使用动态交易策略来对冲风险的想法是后来对复杂证券进行定价的标准方式。

1971 年，默顿的同事保罗·麦卡沃伊 (Paul McAvoy) 问默顿是否愿意在他正在编辑的一本新期刊上发表他对期权价格结果的推导。默顿同意了，但要求推迟出版，直到布莱克-斯科尔斯论文发表。于是，直到1973 年，默顿的论文“理性期权估值理论”才出现在《贝尔经济与管理科学杂志》上。

这就是吸引我到华尔街的那个公式的发现过程。不论你觉得有没有趣，人生就是这样，做不了太多。