光速悖论

戴榕菁

前几天在写“光速不变其实并非一个简单的假设”的英文版“Constant Light Speed in Vacuum was not a Mere Postulation”时想到一个有关光速的悖论，一直没能得到很好的解释，拿来与大家分享一下。

假设在太空中有两束相距为L的具有一个宽度的平行光柱A和B（如图1）,假设L=1c，其中c为真空中的光速，1表示1秒的时间长度以满足量纲要求。有一个长度为L的真空箱以速度V=3c/5在与光线垂直的方向向两束光柱运行（不要被L这个长度吓着，在太空中这不算什么，比物理学家戴森设想的戴森球的尺度小太多了）。真空箱的尾端有一小孔。假设当真空箱的前端碰到光柱B时向尾端的小孔发出一束激光。一秒钟后激光到达小孔。由于光速在真空中不随运动参照系而变，这束激光相对光柱A的速度也是c，因此一秒钟之后，它也应该到达光柱A，但是此时小孔与光柱A之间的距离为V=3c/5 。

也就是说，那束激光同时到达相距将近二十万公里的两个目标。这显然是不可能的。应该如何解释这个悖论？

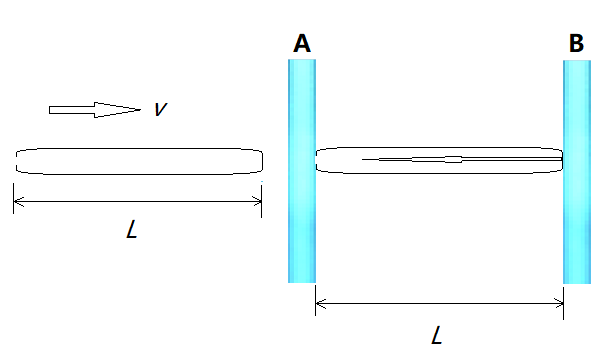
图1关于光速悖论的思想实验示意图

自古希腊的芝诺以来，思想实验一直是人们用来制造悖论故事的有效的工具，而各种悖论故事又可以帮助人们发现人类逻辑的微妙之处或某些逻辑上的缺陷。本文提出这个悖论的目的不是为了否定狭义相对论的光速不变的条件。如我在“光速不变其实并非一个简单的假设”一文中指出的，要想否认真空中光速不变的条件需要否定其它一系列的相关前提。我这里只不过是与大家分享一个我自己在写文章时想到的至今还解释不了的一个悖论而已。相信读者中有很多相对论的专家可以一如既往地一眼就看出这个悖论的答案，欢迎来与大家分享。如果读者中没人解释得了这个悖论，相信它也自然会升级到更广的范围去吸引更多的人来解释。

文中的3/5是一个随意选的数，只是为了表明这个例子具有相对效应的尺度而已。如果有人需要运用洛伦兹变换的话，3/5这个数字运算起来比较方便，用洛伦兹变换开方出来正好是4/5。

顺便提一下，我在“光速不变其实并非一个简单的假设”一文及其英文版“Constant Light Speed in Vacuum was not a Mere Postulation”中都提到由于近些年发现真空中具有能量我们或许有必要验证一下光线是否会与真空能量发生作用。无巧不巧，理论与实验物理学家Hosenfelder在上个星期六的一则视频（https://youtu.be/Bo4al7sNPkE）中提到了这个问题，她说从遥远的星球射来的伽马射线没有出现如在介质中会发生的衍射现象这一点表明光线不会与真空能量发生作用（她的原话说光线在真空中不需要借助能量来运行）。

如果如她所说，来自遥远星球的伽马射线没有表现出任何与介质发生作用的特征的话，我们似乎如她所说可以认定光线不会与真空能量发生作用。

但另一方面，来自遥远的星球的伽马射线没有表现出任何诸如衍射这样的与介质发生作用的现象这一点在我听来似乎也有点奇怪，因为在这途中它几乎可以肯定会经过大量的布满宇宙尘埃的区域，难道都不会对它发生任何影响吗？如果果真如此，是否从另一方面说明gamma射线没有出现衍射现象只能表明它的抗干扰能力强？坦白说，在这方面我是外行，既然专家Hosenfelder说了来自远方的伽马射线没有衍射现象表明光线不会和真空能量发生作用，我们就先接受专家的意见吧。。。。。。