少样本目标检测器通常在样本较多的基础类进行训练,然后在样本较少的新颖类上进行微调,其学习到的模型通常偏向于基础类,并且对新颖类样本的方差敏感。为了解决这个问题,腾讯优图实验室联合武汉大学提出了基于变分特征聚合的少样本目标检测模型 VFA,大幅刷新了 FSOD 指标。本工作已入选 AAAI 2023 Oral。
不同于传统的目标检测问题,少样本目标检测(FSOD)假设我们有许多的基础类样本,但只有少量的新颖类样本。其目标是研究如何将基础类的知识迁移到新颖类,进而提升检测器对新颖类的识别能力。
FSOD 通常遵循两阶段训练范式。在第一阶段,检测器使用丰富的基础类样本进行训练,以学习目标检测任务所需的通用表示,如目标定位和分类。在第二阶段中,检测器仅使用 少量(如 1, 2, 3...)新颖类样本进行微调。然而由于基础类和新颖类样本数量的不平衡,其学习到的模型通常偏向于基础类,进而导致新颖类目标与相似的基础类混淆。此外,由于每个新颖类只有少量样本,模型对新颖类的方差很敏感。例如,随机采样新颖类样本进行多次训练,每次的结果都会有较大的差异。因此十分有必要提升模型在少样本下的鲁棒性。
近期,腾讯优图实验室与武汉大学提出了基于变分特征聚合的少样本目标检测模型 VFA。VFA 的整体结构是基于改进版的元学习目标检测框架 Meta R-CNN++,并提出了两种特征聚合方法:类别无关特征聚合 CAA(Class-Agnostic Aggregation)和变分特征聚合 VFA(Variational Feature Aggregation)。
特征聚合是 FSOD 中的一个关键设计,其定义了 Query 和 Support 样本之间的交互方式。前面的方法如 Meta R-CNN 通常采用类别相关特征聚合 CSA(class-specific aggregation),即同类 Query 和 Support 样本的特征进行特征聚合。与此相反,本文提出的 CAA 允许不同类样本之间的特征聚合。由于 CAA 鼓励模型学习类别无关的表示,其降低了模型对基础类的偏向。此外,不同类之间的交互能够更好地建模类别间的关系,从而降低了类别的混淆。
基于 CAA,本文又提出了 VFA,其采用变分编码器(VAEs)将 Support 样本编码为类的分布,并从学习到的分布中采样新的 Support 特征进行特征融合。相关工作 [1] 指出类内方差(如外观的变化)在不同类之间是相似的,并且可以通过常见的分布进行建模。因此我们可以利用基础类的分布来估计新颖类的分布,进而提高少样本情况下特征聚合的鲁棒性。
VFA 在多个 FSOD 数据集上表现优于目前最好的模型,相关研究已经被 AAAI 2023 录用为 Oral。

论文地址:https://arxiv.org/abs/2301.13411
VFA 模型细节
更强的基线方法:Meta R-CNN++
目前 FSOD 的工作主要可以分为两类:基于元学习(meta learning)的方法和基于微调(fine-tuning)的方法。早期的一些工作证明元学习对 FSOD 是有效的,但基于微调的方法在最近受到越来越多的关注。本文首先建立了一个基于元学习的基线方法 Meta R-CNN++,缩小了两种方法之间的差距,在某些指标上甚至超过了基于微调的方法。
我们首先分析了两种方法在实现上的一些差距,以元学习方法 Meta R-CNN [2] 和基于微调的方法 TFA [3] 为例,虽然这两种方法都遵循两阶段训练范式,TFA 在微调阶段使用额外的技术优化模型:
TFA 冻结了大部分网络参数,只训练最后的分类和回归层,这样模型就不会过度拟合少样本类别。
TFA 不是随机初始化分类层,而是复制基础类的预训练权重,只初始化新颖类的权重。
TFA 采用余弦分类器(cosine classifier)而不是线性分类器。
考虑到 TFA 的成功,我们构建了 Meta R-CNN++。如下表 1 所示,只要我们仔细处理微调阶段,元学习方法也能够取得较好的效果。因此,本文选择 Meta R-CNN++ 作为基线方法。
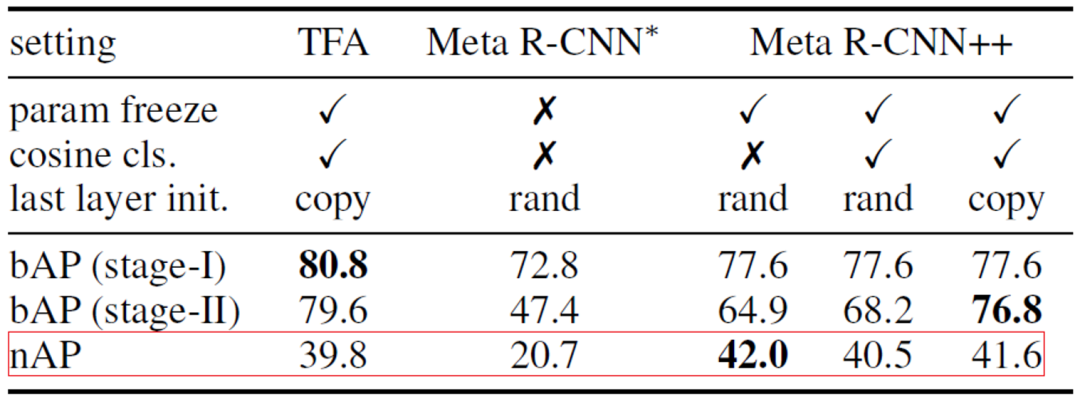 表一:Meta R-CNN 和 TFA 的对比与分析
表一:Meta R-CNN 和 TFA 的对比与分析
类别无关特征聚合 CAA
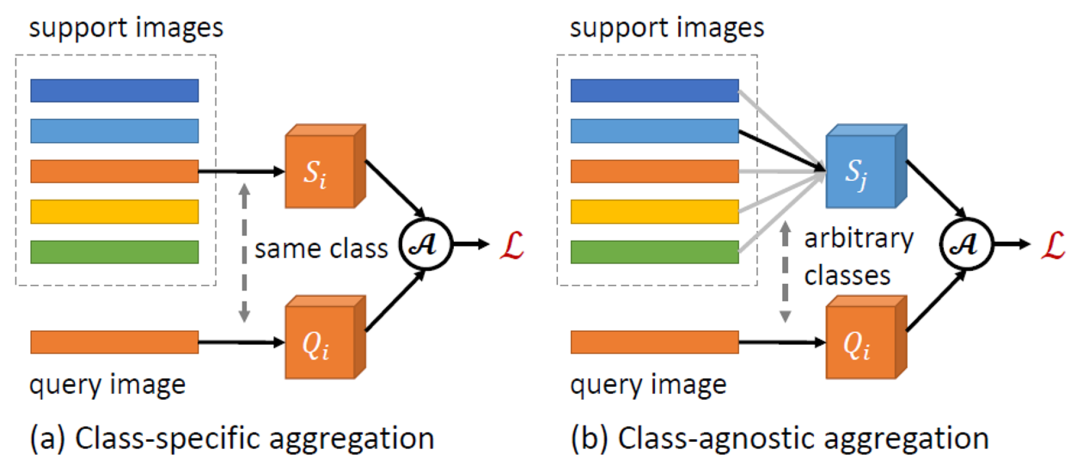 图一:类别无关特征聚合 CAA 示意图
图一:类别无关特征聚合 CAA 示意图
本文提出一个简单而有效的类别无关特征聚合方法 CAA。如上图一所示,CAA 允许不同类之间的特征聚合,进而鼓励模型学习类别无关的表示,从而减少类别间的偏向和类之间的混淆。具体来说,对于类别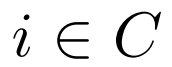 的每个 RoI 特征
的每个 RoI 特征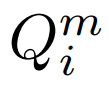 和一组 Support 特征
和一组 Support 特征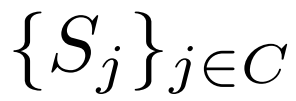 ,我们随机选择一个类的 Support 特征
,我们随机选择一个类的 Support 特征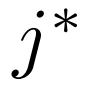 的
的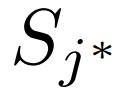 与 Query 特征聚合:
与 Query 特征聚合:
然后我们将聚合特征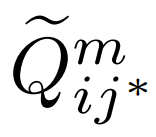 提供给检测子网络
提供给检测子网络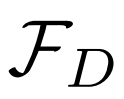 以输出分类得分
以输出分类得分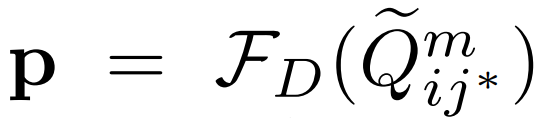 。
。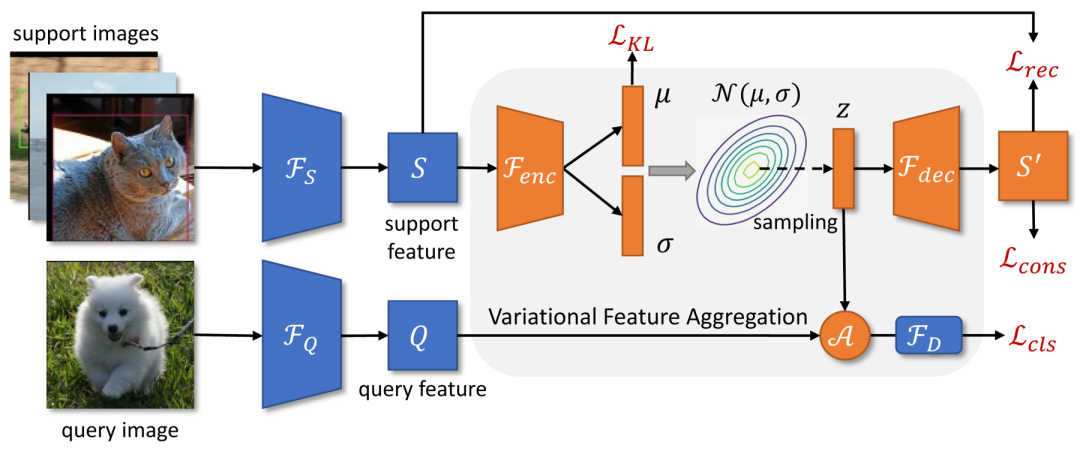 图二 VFA 模型示意图之前的工作通常将 Support 样本编码为单个特征向量来表示类别的中心。然而在样本较少且方差较大的情况下,我们很难对类中心做出准确的估计。在本文中,我们首先将 Support 特征转换为类别的分布。由于估计出的类别分布不偏向于特定样本,因此从分布中采样的特征对样本的方差有较好的鲁棒性。VFA 的框架如上图二所示。
图二 VFA 模型示意图之前的工作通常将 Support 样本编码为单个特征向量来表示类别的中心。然而在样本较少且方差较大的情况下,我们很难对类中心做出准确的估计。在本文中,我们首先将 Support 特征转换为类别的分布。由于估计出的类别分布不偏向于特定样本,因此从分布中采样的特征对样本的方差有较好的鲁棒性。VFA 的框架如上图二所示。
a)变分特征学习。VFA 采用变分自编码器 VAEs [4] 来学习类别的分布。如图二所示,对于一个 Support 特征 S,我们首先使用编码器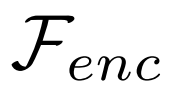 来估计分布的参数
来估计分布的参数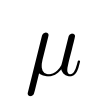 和
和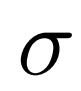 ,接着从分布
,接着从分布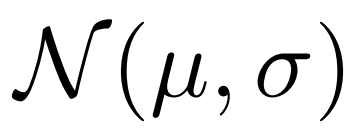 中通过变分推理(variational inference)采样
中通过变分推理(variational inference)采样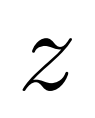 ,最后通过解码器
,最后通过解码器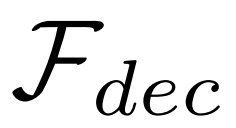 得到重构的 Support 特征
得到重构的 Support 特征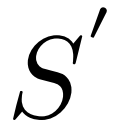 。在优化 VAE 时,除了常见的 KL Loss
。在优化 VAE 时,除了常见的 KL Loss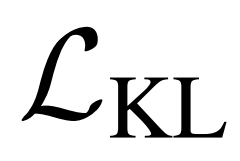 和重构 Loss
和重构 Loss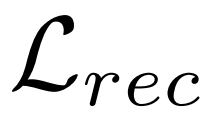 ,本文还使用了一致性 Loss 使得学习到的分布保留类别信息:b)变分特征融合。由于 Support 特征被转换为类别的分布,我们可以从分布中采样特征并与 Query 特征聚合。具体来说,VFA 同样采用类别无关聚合 CAA,但将 Query 特征
,本文还使用了一致性 Loss 使得学习到的分布保留类别信息:b)变分特征融合。由于 Support 特征被转换为类别的分布,我们可以从分布中采样特征并与 Query 特征聚合。具体来说,VFA 同样采用类别无关聚合 CAA,但将 Query 特征 与变分特征
与变分特征 聚合在一起。给定类
聚合在一起。给定类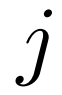 的 Query 特征
的 Query 特征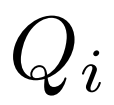 和类
和类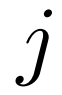 的 Support 特征
的 Support 特征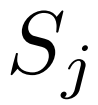 ,我们首先估计其分布
,我们首先估计其分布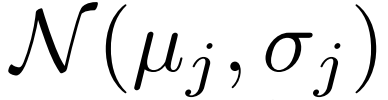 ,并采样变分特征
,并采样变分特征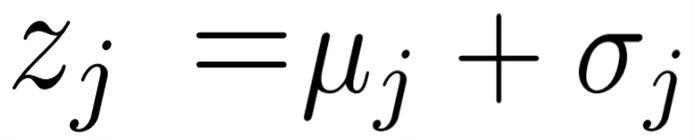 ;然后通过下面的公式将其融合在一起:其中
;然后通过下面的公式将其融合在一起:其中 表示通道乘法,而 sig 是 sigmoid 操作的缩写。在训练阶段,我们随机选择一个 Support 特征
表示通道乘法,而 sig 是 sigmoid 操作的缩写。在训练阶段,我们随机选择一个 Support 特征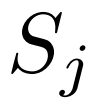 进行聚合;在测试阶段,我们对
进行聚合;在测试阶段,我们对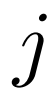 类的
类的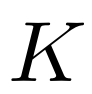 个 Support 特征取平均值
个 Support 特征取平均值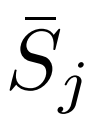 ,并估计分布
,并估计分布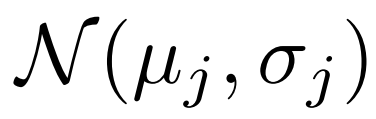 ,其中
,其中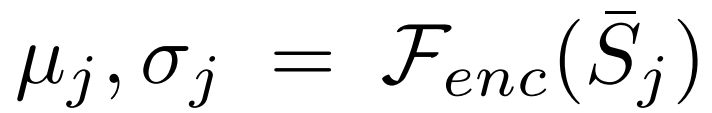 。通常情况下,检测子网络
。通常情况下,检测子网络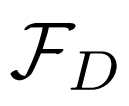 包含一个共享特征提取器
包含一个共享特征提取器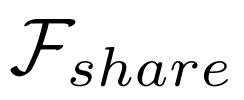 和两个独立的网络:分类子网络
和两个独立的网络:分类子网络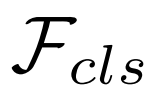 和回归子网络
和回归子网络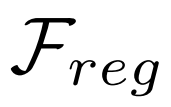 。在前面的工作中,聚合后的特征被输入到检测子网络中进行目标分类和边界框回归。但是分类任务需要平移不变特征,而回归需要平移协变的特征。由于 Support 特征表示的是类别的中心,具有平移不变性,因此聚合后特征会损害回归任务。本文提出一种简单的分类 - 回归任务解耦。让
。在前面的工作中,聚合后的特征被输入到检测子网络中进行目标分类和边界框回归。但是分类任务需要平移不变特征,而回归需要平移协变的特征。由于 Support 特征表示的是类别的中心,具有平移不变性,因此聚合后特征会损害回归任务。本文提出一种简单的分类 - 回归任务解耦。让 和
和 表示原始和聚合后的 Query 特征,之前的方法对这两个任务都采用
表示原始和聚合后的 Query 特征,之前的方法对这两个任务都采用 ,其中分类分数
,其中分类分数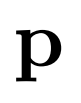 和预测边界框
和预测边界框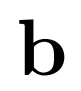 定义为:为了解耦这些任务,我们采用单独的特征提取器并使用原始的 Support 特征
定义为:为了解耦这些任务,我们采用单独的特征提取器并使用原始的 Support 特征 进行边界框回归:我们采用的数据集:PASCAL VOC、 MS COCO。评价指标:新颖类平均精度 nAP、基础类平均精度 bAP。VFA 在两个数据集上都取得了较好的结果。如在 PASCAL VOC 数据集上(下表二),VFA 显著高于之前的方法;VFA 的 1-shot 结果甚至高于一些方法 10-shot 的结果。
进行边界框回归:我们采用的数据集:PASCAL VOC、 MS COCO。评价指标:新颖类平均精度 nAP、基础类平均精度 bAP。VFA 在两个数据集上都取得了较好的结果。如在 PASCAL VOC 数据集上(下表二),VFA 显著高于之前的方法;VFA 的 1-shot 结果甚至高于一些方法 10-shot 的结果。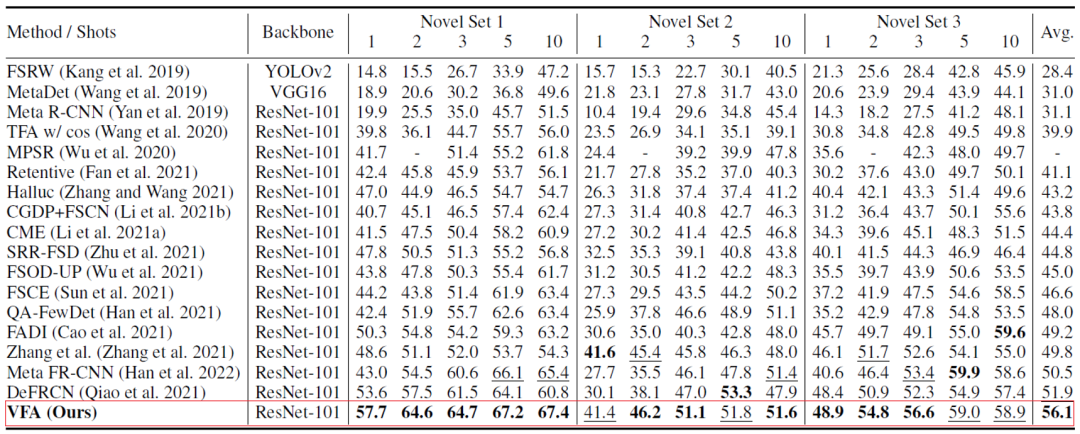 表二 VFA 在 PASCAL VOC 数据集上的效果a)不同模块的作用。如下表三所示,VFA 的不同模块可以共同作用,提升模型的性能。
表二 VFA 在 PASCAL VOC 数据集上的效果a)不同模块的作用。如下表三所示,VFA 的不同模块可以共同作用,提升模型的性能。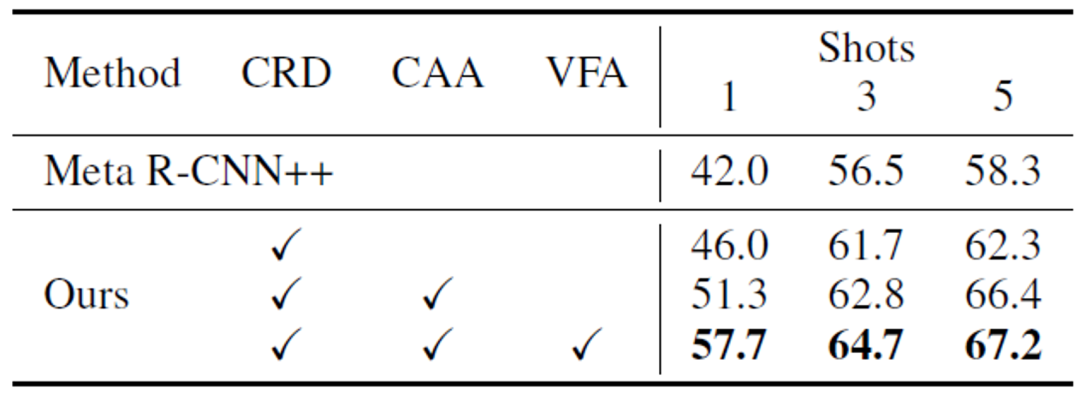 表三 不同模块的作用b) 不同特征聚合方法可视化分析。如下图三所示,CAA 可以减小基础类与新颖类之间的混淆;VFA 在 CAA 的基础上,进一步增强了类间的区分度。
表三 不同模块的作用b) 不同特征聚合方法可视化分析。如下图三所示,CAA 可以减小基础类与新颖类之间的混淆;VFA 在 CAA 的基础上,进一步增强了类间的区分度。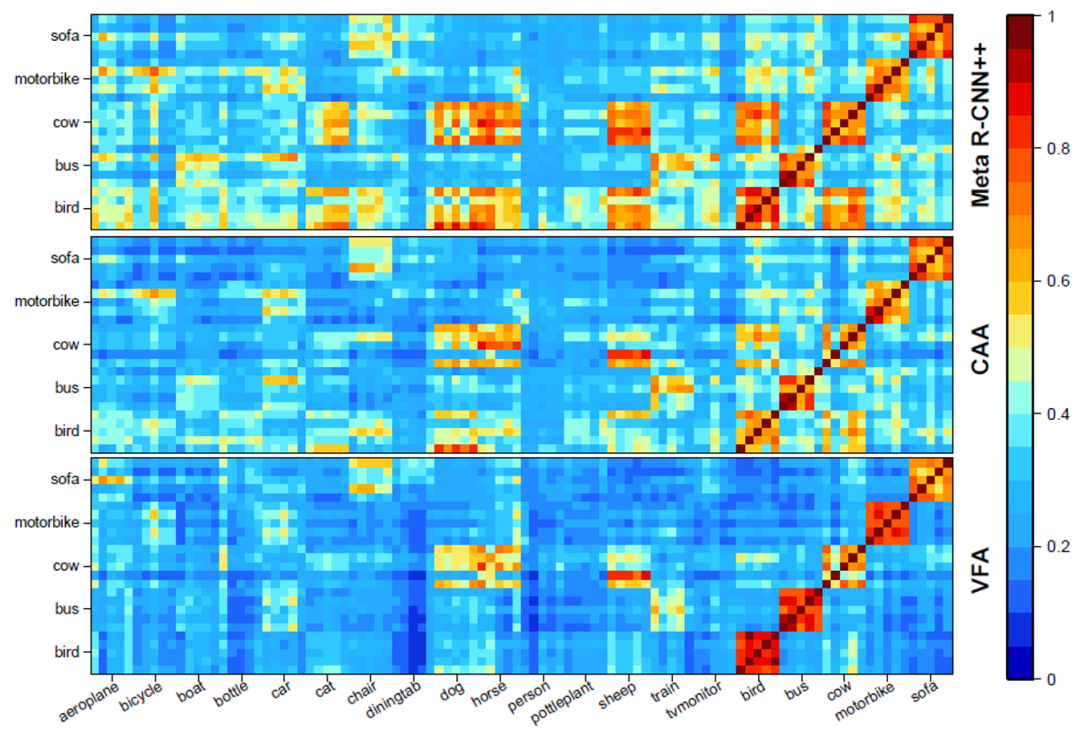 图三 相似矩阵可视化c)更加准确的类别中心点估计。如下图四所示,VFA 可以更加准确的估计出类别的中心。且随着样本数量的减少,估计的准确度逐渐高于基线方法。这也解释了为什么我们的方法在样本少的情况下(K=1)表现的更好。
图三 相似矩阵可视化c)更加准确的类别中心点估计。如下图四所示,VFA 可以更加准确的估计出类别的中心。且随着样本数量的减少,估计的准确度逐渐高于基线方法。这也解释了为什么我们的方法在样本少的情况下(K=1)表现的更好。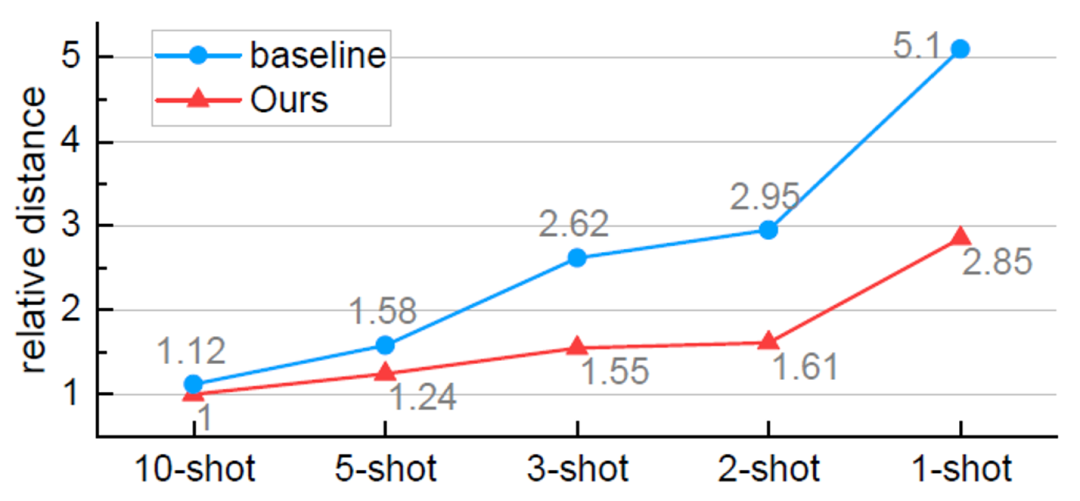 图四 估计的类别中心与真实类别中心间的距离
图四 估计的类别中心与真实类别中心间的距离 图五 可视化结果本文回归了基于元学习的 FSOD 中特征聚合方法,并提出了类别无关特征聚合 CAA 和变分特征聚合 VFA。CAA 可以减少基础类和新颖类之间的类别偏差和混淆;VFA 将样本转换为类别分布以实现更加鲁棒的特征聚合。本文提出的方法在 PASCAL VOC 和 MS COCO 数据集上的实验证明了其有效性。[1]Lin X, Duan Y, Dong Q, et al. Deep variational metric learning [C]//Proceedings of the European Conference on Computer Vision (ECCV). 2018: 689-704.[2]Yan X, Chen Z, Xu A, et al. Meta r-cnn: Towards general solver for instance-level low-shot learning [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 9577-9586.[3]Wang X, Huang T E, Darrell T, et al. Frustratingly simple few-shot object detection [C]//Proceedings of the 37th International Conference on Machine Learning. 2020: 9919-9928.[4]Kingma D P, Welling M. Auto-encoding variational bayes [J]. arXiv preprint arXiv:1312.6114, 2013.
图五 可视化结果本文回归了基于元学习的 FSOD 中特征聚合方法,并提出了类别无关特征聚合 CAA 和变分特征聚合 VFA。CAA 可以减少基础类和新颖类之间的类别偏差和混淆;VFA 将样本转换为类别分布以实现更加鲁棒的特征聚合。本文提出的方法在 PASCAL VOC 和 MS COCO 数据集上的实验证明了其有效性。[1]Lin X, Duan Y, Dong Q, et al. Deep variational metric learning [C]//Proceedings of the European Conference on Computer Vision (ECCV). 2018: 689-704.[2]Yan X, Chen Z, Xu A, et al. Meta r-cnn: Towards general solver for instance-level low-shot learning [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 9577-9586.[3]Wang X, Huang T E, Darrell T, et al. Frustratingly simple few-shot object detection [C]//Proceedings of the 37th International Conference on Machine Learning. 2020: 9919-9928.[4]Kingma D P, Welling M. Auto-encoding variational bayes [J]. arXiv preprint arXiv:1312.6114, 2013.
表一:Meta R-CNN 和 TFA 的对比与分析
图一:类别无关特征聚合 CAA 示意图
的每个 RoI 特征
和一组 Support 特征
,我们随机选择一个类的 Support 特征
的
与 Query 特征聚合: