海归学者发起的公益学术平台
分享信息,整合资源
交流学术,偶尔风月

剪切粘度是决定液体宏观流动最重要的输运特性之一,在化学、机械工程、行星科学以及溶质动力学和反应速率等科学技术的各个领域中都发挥着至关重要的作用。作为一种无处不在的分子液体,水具有非凡而复杂的特性。尽管目前已有大量基于密度泛函理论(DFT)和从头算分子动力学(AIMD)的研究工作,但大多数研究都没有涉及到水的粘度特性。这主要是因为第一性原理准确计算水的粘度需要相当长的模拟时间。近年来,随着深度神经网络、高斯过程等方法的兴起,作为原子模拟的强大工具,机器学习训练势够能达到接近量子力学的精度,有望扩展AIMD的模拟范围,从而达到计算粘度等输运特性所需尺寸的要求。
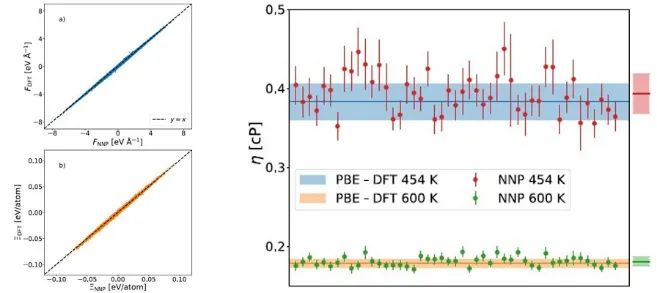
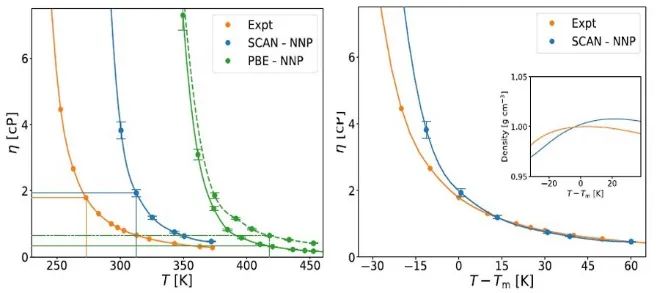
来自意大利国际高等研究院SISSA的Stefano Baroni教授团队,基于密度泛函理论,采用Green-Kubo线性。为达到可接受的统计精度,通常需要较长的模拟时间。针对这一问题,作者使用了深度神经网络势对从头算方法进行了改进。他们首先使用Perdew-Burke-Ernzerhof(PBE)交换关联泛函获得了AIMD结果,对方法进行了验证,其中重点关注了那些对统计数据分析至关重要但经常被忽略的因素。然后,使用由强约束和适当规范(SCAN)泛函生成的数据集训练了第二个NNP。通过比较模拟温度与理论熔点,消除了由于熔化线预测不准确导致的误差,这样对水的剪切粘度的SCAN预测与实验相当吻合。这些结果对未来研究水和其他液体的粘度问题提供了新思路。该文近期发表于npj Computational Materials 8:139(2022),英文标题与摘要如下,点击左下角“阅读原文”可以自由获取论文PDF。
Viscosity in water from first-principles and deep-neural-network simulations
Cesare Malosso, Linfeng Zhang, Roberto Car, Stefano Baroni & Davide Tisi
We report on an extensive study of the viscosity of liquid water at near-ambient conditions, performed within the Green-Kubo theory of linear response and equilibrium ab initio molecular dynamics (AIMD), based on density-functional theory (DFT). In order to cope with the long simulation times necessary to achieve an acceptable statistical accuracy, our ab initio approach is enhanced with deep-neural-network potentials (NNP). This approach is first validated against AIMD results, obtained by using the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional and paying careful attention to crucial, yet often overlooked, aspects of the statistical data analysis. Then, we train a second NNP to a dataset generated from the Strongly Constrained and Appropriately Normed (SCAN) functional. Once the error resulting from the imperfect prediction of the melting line is offset by referring the simulated temperature to the theoretical melting one, our SCAN predictions of the shear viscosity of water are in very good agreement with experiments.