海归学者发起的公益学术平台
分享信息,整合资源
交流学术,偶尔风月

在传统的科学发现过程中,科学家根据由第一原理及经验法则所得的先验知识,结合实验数据以及直觉,获得支配物理规律的方程。牛顿万有引力定律、爱因斯坦质能等效方程、开普勒行星运动定律等物理定律,无不是通过对实验数据理解、归纳与推理揭示的。然而,对于一些尚未完全理解的物理问题,通过回归拟合实验数据的方法十分困难,物理规律的支配方程组集合可能是非常大的。一个典型的例子,是研究对材料受到环境因素的影响,迄今其底层物理规律通常缺乏理解。例如,有机-无机卤化物钙钛矿材料具有提供高性能和经济高效太阳能的潜力,但会在高温、潮湿和光照条件下降解。这个降解问题阻碍了钙钛矿光伏技术的商业化。然而,至今卤化物钙钛矿的降解机制仍不清楚。
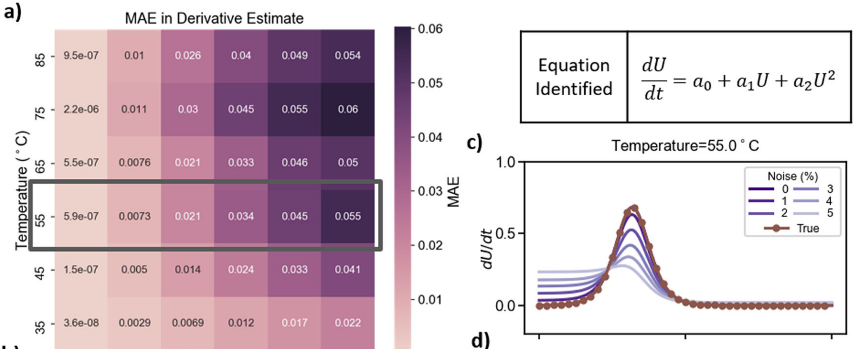
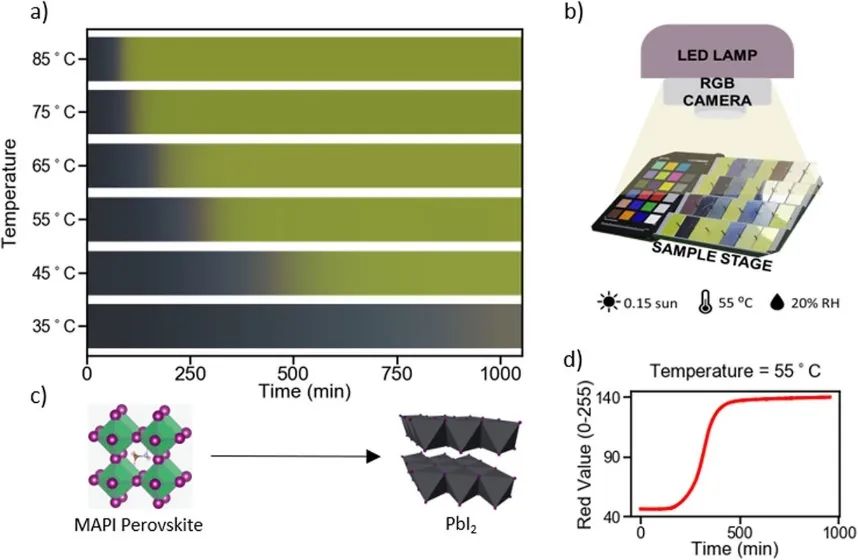
来自美国麻省理工学院的Tonio Buonassisi教授团队,使用机器学习,基于有机-无机甲基铵碘化铅(MAPI)钙钛矿薄膜在环境参数(升温、加湿和光照)下降解的实验数据,推测了蕴含其中的微分方程。该研究除了得到支配钙钛矿材料降解的微分方程外,还提供了有助于设计更稳定的钙钛矿薄膜的建议:可以通过降低材料内部成核点的密度来减少材料降解。作者检验了对实验变动和高斯噪声稳健性的结论,并给出了该方法适用的实验限制条件。该研究展示了机器学习辅助科学发现在实验化学和材料系统中的应用,凸显了其前景和挑战。
该文近期发表于npj Computational Materials 8:72(2022),英文标题与摘要如下,点击左下角“阅读原文”可以自由获取论文PDF。
Discovering equations that govern experimental materials stability under environmental stress using scientific machine learning
Richa Ramesh Naik, Armi Tiihonen, Janak Thapa, Clio Batali, Zhe Liu, Shijing Sun & Tonio Buonassisi
While machine learning (ML) in experimental research has demonstrated impressive predictive capabilities, extracting fungible knowledge representations from experimental data remains an elusive task. In this manuscript, we use ML to infer the underlying differential equation (DE) from experimental data of degrading organic-inorganic methylammonium lead iodide (MAPI) perovskite thin films under environmental stressors (elevated temperature, humidity, and light). Using a sparse regression algorithm, we find that the underlying DE governing MAPI degradation across a broad temperature range of 35 to 85 °C is described minimally by a second-order polynomial. This DE corresponds to the Verhulst logistic function, which describes reaction kinetics analogous to self-propagating reactions. We examine the robustness of our conclusions to experimental variance and Gaussian noise and describe the experimental limits within which this methodology can be applied. Our study highlights the promise and challenges associated with ML-aided scientific discovery by demonstrating its application in experimental chemical and materials systems.