域适应中的域索引：定义、方法、理论和可解释性

公众号新闻

2023-05-13 11:05

©作者 | 王灏

单位 | 罗格斯大学

论文标题：

Domain-Indexing Variational Bayes: Interpretable Domain Index for Domain Adaptation

论文链接：

https://arxiv.org/pdf/2302.02561.pdf

http://wanghao.in/paper/ICLR23_VDI.pdf

OpenReview:

https://openreview.net/forum?id=pxStyaf2oJ5

代码链接：

https://github.com/wang-ML-Lab/VDI

YouTube Video:

https://www.youtube.com/watch?v=xARD4VG19ec

Bilibili Video:

https://www.bilibili.com/video/BV13N411w734/

来给大家介绍一下我们被接收为 ICLR Spotlight 的新工作。这个 work 从 2021 年春开始一直做到 2022 年秋，中间克服了许多技术障碍，没想到第一次投稿就好评如潮（分数 8886），也恭喜子昊的坚持得到回报。

这篇工作的核心贡献在于，正式定义了 domain adaptation 中的域索引（domain index），精心设计了推断（infer）domain index 的算法（variational domain indexing，即 VDI），并且证明了我们的算法可以推断出最优的 domain index。由于推断出来的 domain index 带来的 free lunch，domain adaptation 的性能也得到了提高。

什么是 domain index：domain index 的说法最早在我们的 ICML 2020 论文“Continuously Indexed Domain Adaptation”（CIDA）中提出（有兴趣的看官欢迎移步我们讲 CIDA 的知乎帖子）。最直观的例子就是在医疗应用里面，不同年龄的人可以看成是不同的 domain，而这个“年龄”其实就是 domain 的一个索引（index），也就是我们说的 domain index（域索引）。如下图。

有意思的是，domain index 其实是一个连续的概念，所以自然而然地包含了 domain 的远近信息。比如上面说的“年龄”可以作为一个一维的 domain index，年龄 18 和 19 距离很近，而 18 和 80 却距离很远。我们之前在 CIDA（大致的 CIDA 模型如下图）上的实验发现，如果已知这个 domain index，我们可以很好地做到连续域上的 domain adaptation，从而大幅提高准确率。

比如把模型从年龄 0~20 的病人（source domains），adapt 到年龄 20~80 的病人（target domains），或者从年龄 0~15 以及 50~80 的病人（source domains），adapt 到年龄 15~50 的病人（target domains），如下图。

那么问题来了，如果这个 domain index 是未知的，咋办？最理想的情况当然是，我们能够把这个 domain index 作为隐变量（latent variable），通过无监督（unsupervised）的方式把它推断（infer）出来。如果这个方案可行，我们就免费拿到了一个重要的额外的信息，从而既可以提高 domain adaptation 的准确率，又能提高它的可解释性。

Domain Index 的正式定义：在推断 domain index 前，我们要先定义清楚，什么才算是 domain index，然后才能设计推断它的方法。

这里我们首先引入了两种 domain index，local domain index（用 u 表示）和 global domain index（用 β 表示）。我们规定，虽然同一个 domain 里的不同数据点（data point）可以有不同的 local domain index，但是同一个 domain 里的所有数据的 global domain index 必须是是相同的。

也就是说，local domain index 是一个 instance-level 的变量，而 global domain index 是一个 domain-level 的变量。下面的图是一个具体的例子，展示了 global domain index β、local domain index u、数据 x 之间的关系。

那么符合什么条件的 u 和 beta 才能被叫做 domain index 呢？我们定义了三个条件（这里 x 表示数据，y 表示标签，z 表示 x 经过 encoder 后得到的 encoding）：

1. z 和 β 的条件独立：Encoding z 和 global domain index β 是条件独立的。换句话说，他们的互信息 I(z; β) 必须是 0。

2. 保留 x 的信息：Encoding z，global domain index β，和 local domain index u 这三组变量，比如尽可能地保留数据 x 的信息。换句话说，他们的互信息 I((x; u, β, z) 必须达到最大。

3. z 对标签 y 的敏感度：Encoding z 要尽可能保留标签 y 的信息（这样才能提高预测y的准确率）。这意味着他们的互信息 I(z; y) 必须达到最大。

如果 β 和 u 满足上述三个条件，我们就把它们分别称为 global domain index 和 local domain index。这三个条件可以用下面的数学公式表示：

方法的整体思路：定义完 domain index 后，下一个问题自然就是，如何能在无监督（完全不知道 domain index）的情况下，有效地推断出符合上面三段定义的 domain index β 和 u 呢？这时，就要请出 adversarial Bayesian deep learning model（对 Bayesian deep learning 感兴趣的同学可以看看我们之前的帖子）来解决这个问题。

在 Bayesian deep learning 里面，或者更加传统的 probabilistic graphical model 里面，我们会分两步走：第一步是首先假设一下已知变量（observed variable）是如何从隐变量（latent variable，即未知的变量）一步步生成的。我们一般把这个叫做生成过程（generative process）。

然后第二步，就是通过贝叶斯推断（Bayesian inference）的方式来根据已知变量来倒推隐变量。在我们目前的问题里，数据 x 以及标签 y 都是已知变量，而我们的 encoding z 以及 domain index β 和 u 则是隐变量。那么很自然，我们的目的就是已知各个 domain 里的数据 x 以及标签 y，然后想推断出 encoding z 以及 domain index β 和 u。注意，在 domain adaptation 里面，只有 source domain 才有已知的标签 y。target domain 只有数据 x。

生成过程：根据这个整体思路，我们就首先假设一下各个变量生成过程（如下图左边）：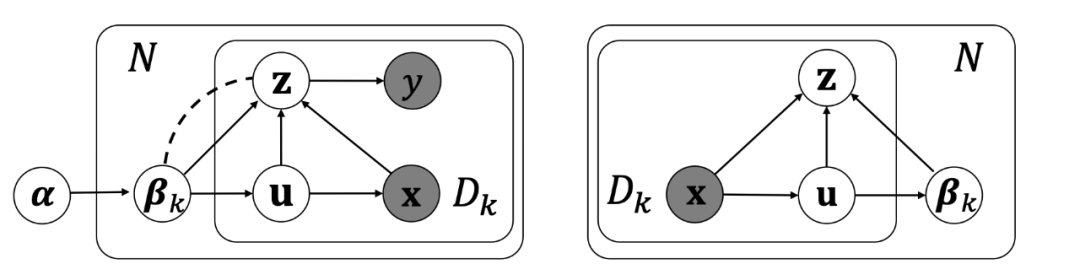

对于每个 domain k（k=1,2,...,N）：

从高斯分布 p(β|α) 中生成一个 global domain index β_k，
对于 domain k 中的每个数据点 i（i=1,2,...,D_k）：

从高斯分布 p(u_i | β_k) 中生成一个 local domain index u_i，
从高斯分布 p(x_i | u_i) 中生成数据 x_i，
从高斯分布 p(z_i | x_i, u_i, β_k) 中生成 encoding z_i，
从分布 p(y_i | z_i) 中生成标签 y_i。

用变分分布估计后验概率：有了这个生成过程，我们就可以开始思考如何推断（infer）出每个数据 x_i 对应的 encoding z_i 及其 domain index β 和 u。我们首先会先构造一些变分分布（variational distribution），通过学些这些变分分布来推断 z_i、β 和 u。比如，如果我们会学会了变分分布 q(u_i | x_i)，那么，给定一个数据 x_i，我们就能根据 q(u_i | x_i) 得到 local domain index u_i 了。

在我们的方法里面我们一共定义了 3 个变分分布：q(u_i | x_i)，q(β_k | {u})，和 q(z_i | x_i, u_i, β_k)。这里对应着上图的右边。在这几个分布里面，比较关键的是分布 q(β_k | {u})，它会对同一个 domain 下所有数据的 local domain index 做一个聚合（aggregation），来推断这个 domain 的 global domain index。

注意每个数据都有自己的不同的 local domain index，而同一个 domain 里的所有数据只共享同一个 global domain index。这里的 {u} 的大括号表示的是同一个 domain 里所有 data 对应的所有 local domain index u 组成的集合。在推断 global domain index 时，我们还在 u 的集合上应用了 optimal transport，有兴趣的同学可以看下论文原文的细节。

Evidence Lower Bound (ELBO)：接下来就是用 ELBO 把 5 个生成分布 p(β | α)，p(u_i | β_k)，p(x_i | u_i)，p(z_i | x_i, u_i, β_k)，p(y_i | z_i) 和 3 个变分分布 q(u_i | x_i)，q(β_k | {u})，q(z_i | x_i, u_i, β_k) 串成下面的目标函数：

从变分（variational inference）的角度，最大化上面的 ELBO，等价于在寻找最优的变分分布 q(u_i | x_i)，q(β_k | {u})，q(z_i | x_i, u_i, β_k) 来估计 u_i，β_k，和 z_i 的真实分布。

上面的目标函数可能有点冗长难懂，直接看下图可能会好些。直观地讲，我们可以把优化这个 ELBO，看成学习很多子网络来对输入数据 x 进行编码（encode）和重构（reconstruct）的过程，关键在于，在这个编码和重构的过程中，需要聪明地把 domain index β 和 u 建模进去。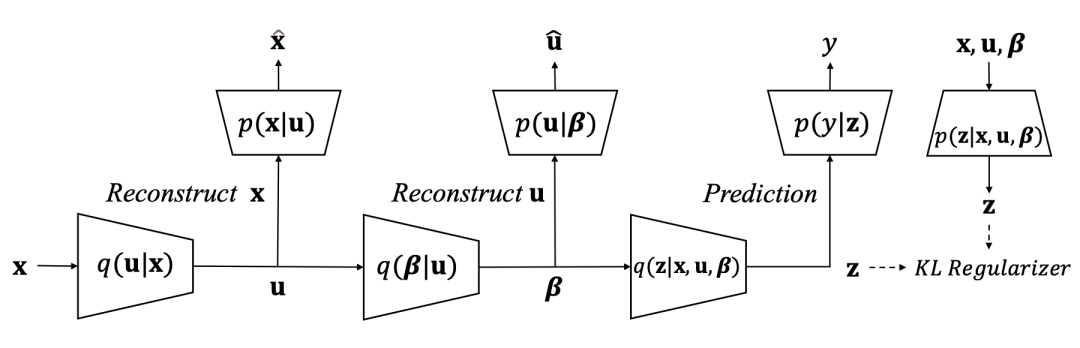

对贝叶斯推断（Bayesian Inference）熟悉的同学可能已经发现了，这个其实就是我们之前说的（广义的）贝叶斯深度学习（Bayesian Deep Learning）的思路：用深度模块（deep component）来处理高维信号 x（比如图片），然后用概率图模块（graphical component）来表示各个随机变量之间的条件概率关系（比如图片 x 及其对应的 encoding z 和 domain index β、u 的关系）。

回到 Domain Index 的三段定义：讲到这里，眼尖的同学可能会发现，虽然最大化这个 ELBO 目标函数确实可能可以符合前面说的 domain index 的三个要求中的后两个，即保留 x 的信息（最大化互信息 I((x; u, β, z)）和 z 对标签 y 的敏感度（最大化互信息I(z; y)），但是却忽略了第一个要求，即 z 和 β 的条件独立（互信息 I(z; β)=0）。

为了满足第一个要求，我们需要借鉴对抗域迁移（adversarial domain adaptation）的思想，在上图的基础上，再加上一个 discriminator，然后对抗地（adversarially）训练整个网络，使得 encoder 能把不同 domain 的 x 映射到一个 encoding 空间，然后让这个 discriminator 无法从他们的 encoding z 来分辨出数据是来自于哪个 domain 的。

我们把这个操作叫做 encoding 的对齐（alignment），即把不同的 domain 的 encoding 分布对齐起来，让他们互相重叠，这样就可以方便不同 domain 共享一个 predictor 了（比如分类器或者回归器）。加上 discriminator 之后的神经网络架构如下：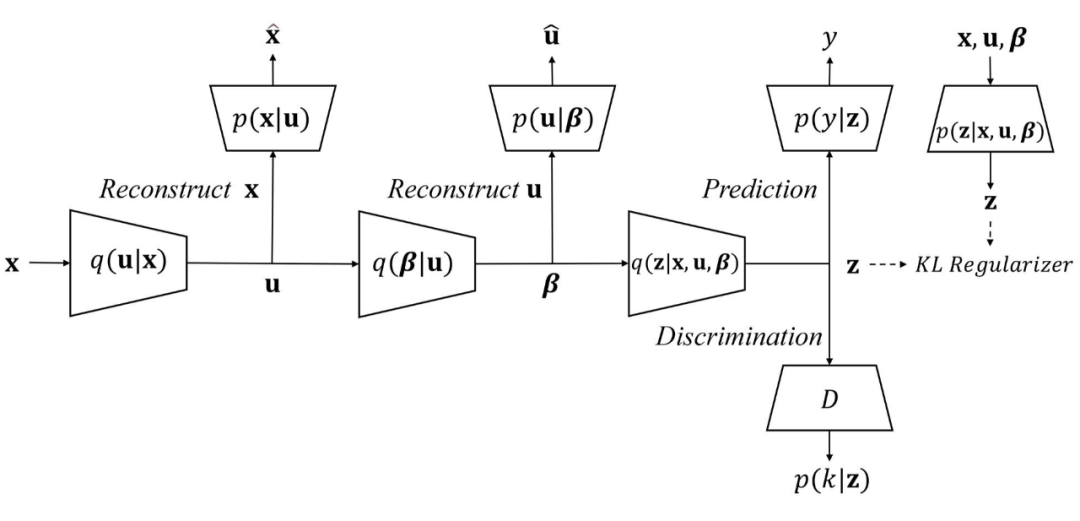

最终的目标函数：相应地，我们最终的目标函数也从一个简单的优化问题（最大化 ELBO）变成了一个 minimax game：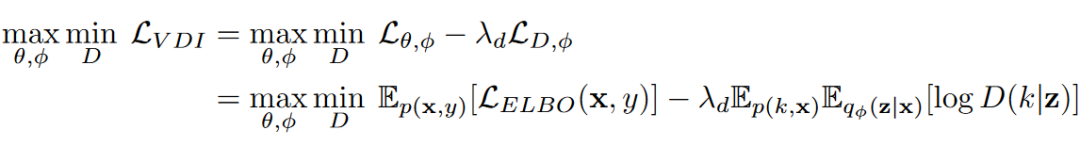

理论保障：有趣的是，我们可以严格地证明，上面的目标函数的全局最优点正好就可以同时满足我们对 domain index 的三段定义：即保留 x 的信息（最大化互信息 I((x; u, β, z)）、z 对标签 y 的敏感度（最大化互信息 I(z; y)）、z 和 β 的条件独立（互信息 I(z; β)=0）。

学到了啥有意思的 domain index：既然有了理论保障，那么接下来我们可以看一下，如果按照上面的方法训练模型，我们能推断出来什么样的 global domain index 呢？我们用的第一个数据集是之前 CIDA 用的 Circle 数据集。这个数据集包含了 30 个 domain，如下图所示。

左下图是用颜色标记了 domain index，我们可以看到颜色是渐变的，也就是说 ground-truth 的 domain index 是从 1 到 30。绿色框里表示的是 6 个 source domain，其他部分为 target domain。右下图是用蓝色和红色标记了标签（label），可以看出来这是个二分类的数据集，蓝色表示正例，红色表示负例。

下面的图展示了我们的 VDI 学习到的 domain index 和 ground-truth domain index 的对比。可以看到，我们学到的 domain index 和真正的 domain index 是高度吻合的，correlation 达到了 0.97。有趣的是，跟 CIDA 不一样，我们在训练 VDI 过程中，并没有用到任何的 domain index，所有的 domain index 都是 VDI 模型自己以无监督的方式推断出来的。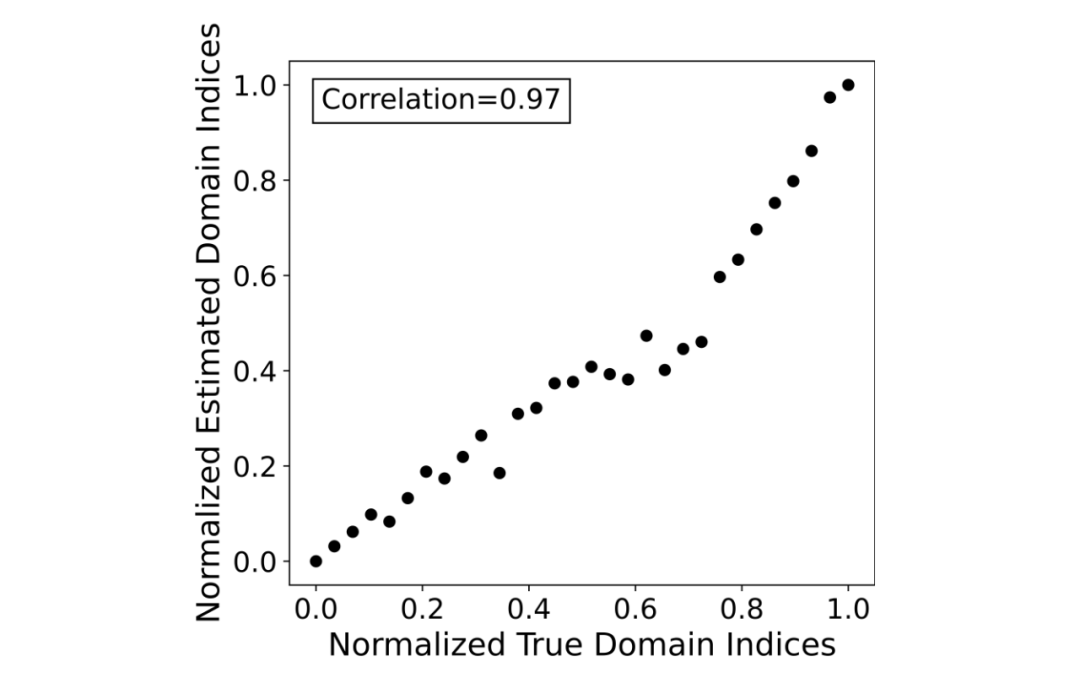

除了 Circle 这个 toy dataset，我们还测试了现实的数据集。比如之前我们在 GRDA 构建的 TPT-48 温度预测数据集。这个数据集有美国大陆 48 个州的每月气温。这里的任务（task）是，根据前 6 个月的气温，预测后 6 个月的气温（如下图左边）。

我们把一部分州的数据作为 source domain（如下图黑底白字的州），然后把其他州作为 target domain（如下图白底黑字的州）。我们把 target domain 分成 3 个层级，level-1、level-2、和 level-3 的 target domain 分别表示离 source domain 最近、次近、和最远的 target domain。

有意思的是，即使在无监督（未知正确的 domain index）的情况下，我们的 VDI 依然能够学出有意义的 domain index。比如下图左边，我们画出来 VDI 学出来的 2 维的 domain index β。下面每个点的坐标位置表示的是我们 VDI 学到的 2 维domain index，而颜色则表示对应的 domain（州）真实的纬度。

我们可以看到，我们 domain index 的第一维（横轴）和真实的每个州的纬度高度吻合。比如纽约（NY）和新泽西（NJ）纬度距离比较近，而且都在比较北边（如下面的右图），那么对应的，他们的 domain index 也很接近。相反，佛罗里达（FL）离 NY 和 NJ 的纬度距离都比较远，对应地，它的 domain index 也离 NY 和 NJ 比较远。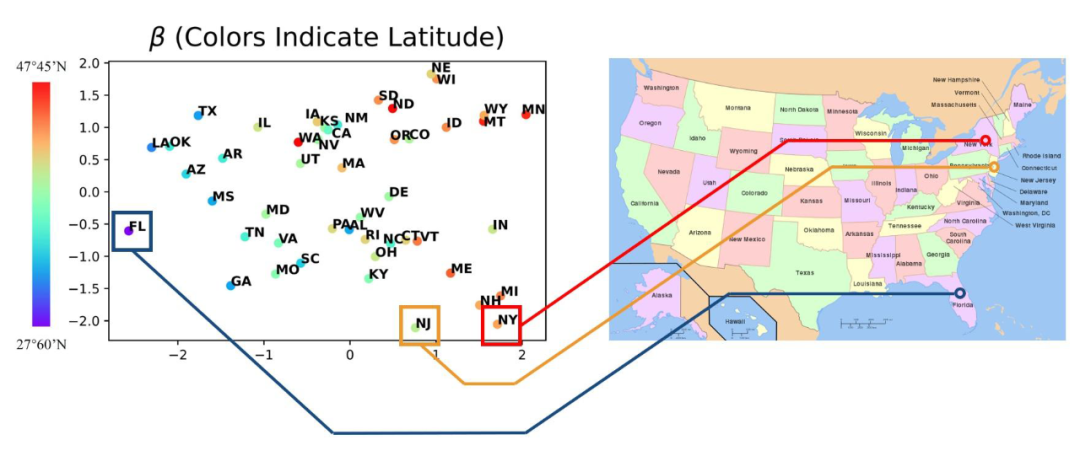

另一个真实数据集是 CompCar，CompCar 里包含了各种车的照片，这些照片有 2 维真实的 domain index，拍照的角度（比如正面照、侧面照、后面照等等）以及出厂年份（比如 2009）。类似地，我们把 VDI 学到的 2 维 domain index 画到下图。

下面每个点的坐标位置表示的是我们 VDI 学到的 domain index，而颜色则表示真实的拍照角度（左图）和出厂年份（右图）。可以看到，即使是在无监督的情况下，我们学出来的 domain index 依然和真实的拍照角度和出厂年份高度相关。

提高 domain adaptation 准确率：当然除了能学出有意思的 domain index，VDI 自然可以利用这些学到的 domain index，来提高 domain adaptation 的准确度。下面的表格是 TPT-48 的温度预测误差（MSE）对比。我们可以看到 VDI 几乎在所有层级（level）的 target domain 都能有准确率的提高。

写在最后：熟悉的同学可能可以看出来，这个 VDI 其实有点像是我们 ICML’20 的 “Continuously Indexed Domain Adaptation”（CIDA）的逆问题，同时也可以看成是和 CIDA 这类算法的互补的问题。

CIDA:

http://wanghao.in/paper/ICML20_CIDA.pdf

CIDA 是想通过已知的 domain index 来提高连续域 adaptation 的准确度，而 VDI 则解决了一个更 general 的问题，也就是当这个 domain index 未知的时候，应该如何去推断出来。而且一旦推断出来 domain index，我们就可以放心地继续使用 CIDA 来实现连续域（甚至是传统的离散域）的 adaptation 准确率的提升了。

还是那句话，希望大家看了之后能够有所启发，没有启发的话，不是子昊同学这个工作做的不好，而是我这个帖子写得不好，所以也请轻拍：）

更多阅读