生成扩散模型漫谈：构建ODE的一般步骤（下）

2023-01-12 14:01

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

上周笔者写了《生成扩散模型漫谈：构建ODE的一般步骤（上）》，本以为已经窥见了构建 ODE 扩散模型的一般规律，结果不久后评论区大神 @gaohuazuo 就给出了一个构建格林函数更高效、更直观的方案，让笔者自愧不如。再联想起之前大神之前在《生成扩散模型漫谈：“硬刚”扩散ODE》同样也给出了一个关于扩散 ODE 的精彩描述（间接启发了上一篇文章的结果），大神的洞察力不得不让人叹服。

经过讨论和思考，笔者发现大神的思路本质上就是一阶偏微分方程的特征线法，通过构造特定的向量场保证初值条件，然后通过求解微分方程保证终值条件，同时保证了初值和终值条件，真的非常巧妙！最后，笔者将自己的收获总结成此文，作为上一篇的后续。

前情回顾

简单回顾一下上一篇文章的结果。假设随机变量连续地变换成，其变化规律服从 ODE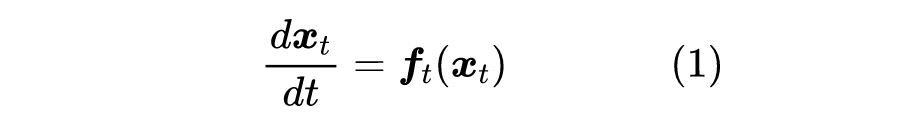

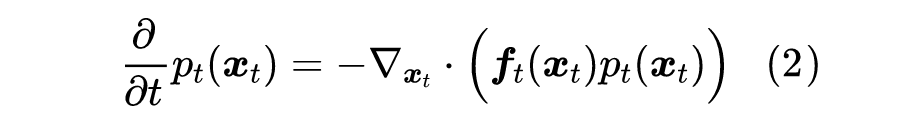
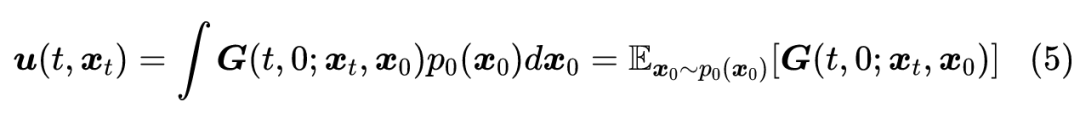
那么对应的时刻的分布服从“连续性方程”：

记

，那么连续性方程可以简写成

为了求解这个方程，可以用格林函数的思想，即先求解

那么

就是满足约束条件的解之一。

几何直观

所谓格林函数，其实思想很简单，它就是说我们先不要着急解决复杂数据生成，我们先假设要生成的数据只有一个点，先解决这单个数据点的生成问题。有的读者想这不是很简单吗？直接就完事了？当然不是这么简单，我们需要的是连续的、渐变的生成，如下图所示，就是上的任意一点，都沿着一条光滑轨迹运行到的上：

▲ 格林函数示意图。图中，在处的每个点，都沿着特定的轨迹运行到处的一个点，除了公共点外，轨迹之间无重叠，这些轨迹就是格林函数的场线

而我们的目的，只是构造一个生成模型出来，所以我们原则上并不在乎轨迹的形状如何，只要它们都穿过，那么，我们可以人为地选择我们喜欢的、经过的一个轨迹簇，记为

再次强调，这代表着以为起点、以为终点的一个轨迹簇，轨迹自变量、因变量分别为，起点是固定不变的，终点是可以任意变化的，轨迹的形状是无所谓的，我们可以选择直线、抛物线等等。

现在我们对式（6）两边求导，由于是可以随意变化的，它相当于微分方程的积分常数，对它求导就等于，于是我们有

对比式（1），我们就得到

这里将原本的记号替换为了，以标记轨线具有公共点。也就是说，这样构造出来的力场所对应的 ODE 轨迹，必然是经过的，这就保证了格林函数的初值条件。

特征线法

既然初值条件有保证了，那么我们不妨要求更多一点：再保证一下终值条件。终值条件也就是希望时的分布是跟无关的简单分布。上一篇文章的求解框架的主要缺点，就是无法直接保证终值分布的简单性，只能通过事后分析来研究。这篇文章的思路则是直接通过设计特定的来保证初值条件，然后就有剩余空间来保证终值条件了。而且，同时保证了初、终值后，在满足连续性方程（2）的前提下，积分条件是自然满足的。

用数学的方式说，我们就是要在给定和的前提下，去求解方程（2），这是一个一阶偏微分方程，可以通过“特征线法”求解，其理论介绍可以参考笔者之前写的《一阶偏微分方程的特征线法》[1]。首先，我们将方程（2）等价地改写成

同前面类似，由于接下来是在给定起点进行求解，所以上式将替换为，以标记这是起点为的解。

特征线法的思路，是先在某条特定的轨迹上考虑偏微分方程的解，这可以将偏微分转化为常微分，降低求解难度。具体来说，我们假设是的函数，在方程（1）的轨线上求解。此时由于成立方程（1），将上式左端的替换为后，左端正好是的全微分，所以此时有

注意，此时所有的应当被替换为对应的的函数，这理论上可以从轨迹方程（6）解出。替换后，上式的、都是纯粹的函数，所以上式只是关于的一个线性常微分方程，可以解得

代入终值条件，得到，即

把轨迹方程（6）的代入，就得到一个只含有的函数，便是最终要求解的格林函数了，相应地有

。

训练目标

有了格林函数，我们就可以得到

于是

根据《生成扩散模型漫谈：一般框架之SDE篇》中构建得分匹配目标的方法，可以构建训练目标

它跟《Flow Matching for Generative Modeling》[2]所给出的“Conditional Flow Matching”形式上是一致的，后面我们还会看到，该论文的结果都可以从本文的方法推出。训练完成后，就可以通过求解方程来生成样本了。从这个训练目标也可以看出，我们对的要求是易于采样就行了。

一些例子

可能前面的抽象结果对大家来说还是不大好理解，接下来我们来给出一些具体例子，以便加深大家对这个框架的直观理解。至于特征线法本身，笔者在《一阶偏微分方程的特征线法》[1] 也说过，一开始笔者也觉得特征线法像是“变魔术”一样难以捉摸，按照步骤操作似乎不困难，但总把握不住关键之处，理解它需要一个反复斟酌的思考过程，无法进一步代劳了。

直线轨迹

作为最简单的例子，我们假设是沿着直线轨迹变为，简单起见我们还可以将 T 设为 1，这不会损失一般性，那么的方程可以写为

根据式（8），有

此时，根据式（12）就有

代入式（16）中的，得到

特别地，如果是标准正态分布，那么上式实则意味着

，这正好是常见的高斯扩散模型之一。这个框架的新结果，是允许我们选择更一般的先验分布，比如均匀分布。另外在介绍得分匹配（15）时也已经说了，对我们只需要知道它的采样方式就行了，而上式告诉我们只需要先验分布易于采样就行，因为：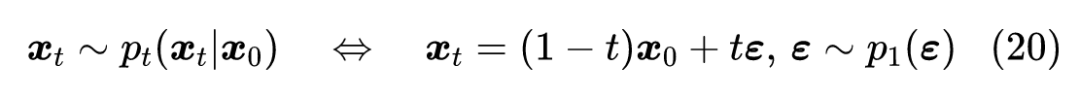

效果演示

注意，我们假设从到的轨迹是一条直线，这仅仅是对于单点生成的，也就是格林函数解。当通过格林函数叠加出一般分布对应的的力场时，其生成轨迹就不再是直线了。

下图演示了先验分布为均匀分布时多点生成的轨线图：

▲ 单点生成

▲ 两点生成

▲ 三点生成

参考作图代码：

 1import numpy as np
 2from scipy.integrate import odeint
 3import matplotlib
 4import matplotlib.pyplot as plt
 5matplotlib.rc('text', usetex=True)
 6matplotlib.rcParams['text.latex.preamble']=[r"\usepackage{amsmath}"]
 7
 8prior = lambda x: 0.5 if 2 >= x >= 0 else 0
 9p = lambda xt, x0, t: prior((xt - x0) / t + x0) / t
10f = lambda xt, x0, t: (xt - x0) / t
11
12def f_full(xt, t):
13    x0s = [0.5, 0.5, 1.2, 1.7]  # 0.5出现两次，代表其频率是其余的两倍
14    fs = np.array([f(xt, x0, t) for x0 in x0s]).reshape(-1)
15    ps = np.array([p(xt, x0, t) for x0 in x0s]).reshape(-1)
16    return (fs * ps).sum() / (ps.sum() + 1e-8)
17
18for x1 in np.arange(0.01, 1.99, 0.10999/2):
19    ts = np.arange(1, 0, -0.001)
20    xs = odeint(f_full, x1, ts).reshape(-1)[::-1]
21    ts = ts[::-1]
22    if abs(xs[0] - 0.5) < 0.1:
23        _ = plt.plot(ts, xs, color='skyblue')
24    elif abs(xs[0] - 1.2) < 0.1:
25        _ = plt.plot(ts, xs, color='orange')
26    else:
27        _ = plt.plot(ts, xs, color='limegreen')
28
29plt.xlabel('$t$')
30plt.ylabel(r'$\boldsymbol{x}$')
31plt.show()

一般推广

其实上面的结果还可以一般地推广到

这里的是任意满足的函数，是任意满足的单调递增函数。根据式（8），有

这也等价于《Flow Matching for Generative Modeling》[2] 中的式（15），此时，根据式（12）就有

代入，最终结果是

这是关于线性 ODE 扩散的一般结果，包含高斯扩散，也允许使用非高斯的先验分布。

再复杂些？

前面的例子，都是通过（的某个变换）与的简单线性插值（插值权重纯粹是的函数）来构建的变化轨迹。那么一个很自然的问题就是：可不可以考虑更复杂的轨迹呢？

理论上可以，但是更高的复杂度意味着隐含了更多的假设，而我们通常很难检验目标数据是否支持这些假设，因此通常都不考虑更复杂的轨迹了。此外，对于更复杂的轨迹，解析求解的难度通常也更高，不管是理论还是实验，都难以操作下去。

更重要的一点的，我们目前所假设的轨迹，仅仅是单点生成的轨迹而已，前面已经演示了，即便假设为直线，多点生成依然会导致复杂的曲线。所以，如果单点生成的轨迹都假设得不必要的复杂，那么可以想像多点生成的轨迹复杂度将会奇高，模型可能会极度不稳定。

文章小结

接着上一篇文章的内容，本文再次讨论了 ODE 式扩散模型的构建思路。这一次我们从几何直观出发，通过构造特定的向量场保证结果满足初值分布条件，然后通过求解微分方程保证终值分布条件，得到一个同时满足初值和终值条件的格林函数。特别地，该方法允许我们使用任意简单分布作为先验分布，摆脱以往对高斯分布的依赖来构建扩散模型。