对称性破缺与复杂性的涌现有何关系?在几十年的研究进程中,诺奖得主、圣塔菲研究所发起人菲利普·安德森(Philip Anderson)从复杂系统的对称性破缺中列举了四个关键原则:涌现性、阻挫随机函数(frustrated random functions)、自主性和广义刚性(generalized rigidity)。安德森四原则是演化功能涌现的先决条件。圣塔菲研究所现任所长 David Krakauer 撰文总结了这些观点,并简要讨论了近期与功能对称性破缺相关概念的扩展,包括信息、计算和因果。
关键词:复杂系统,涌现,对称性破缺,耗散结构理论,自旋玻璃David C. Krakauer | 作者
刘志航 | 译者
刘培源 | 审校
梁金 | 编辑
论文题目:
Symmetry–simplicity, broken symmetry–complexity
论文链接:
https://royalsocietypublishing.org/doi/10.1098/rsfs.2022.0075
复杂现象的涌现在两种情况下有可能出现:一是当基本的物理对称性被打破时;二是当选择特定的基态(ground states)来执行机械工作和存储适应性信息时。在几十年的研究进程中,菲利普·安德森(Philip Anderson)从复杂系统的对称性破缺(broken symmetry)中列举了几个关键原则。这些原则包括涌现性、阻挫随机函数(frustrated random functions)、自主性和广义刚性(generalized rigidity)。安德森四原则是演化功能涌现的先决条件。David Krakauer 撰文总结了这些观点,并简要讨论了近期与功能对称性破缺相关概念的扩展,包括信息、计算和因果关系。
“在此之前的讨论是关于装饰和晶体中存在的几何对称性,是时候结束讨论了。这最后一次讲座的主要目标是展示在基本的物理和数学问题中对称性原则的作用,并从这些和其之前的应用中提出对原则本身的最终普遍陈述。”
“于是我开始寻找日常世界的'Aufbauprinzips(结构原则)'。我很钦佩 Frohlich 的关于电介质理论的书,因为它采取了同样的观点;我在早期的铁电体工作中遇到了它。更为重要的是,我开始认识到对称性破缺概念的重要性,这一直是我生活中的长期兴趣。对称性破缺是“多者异也”(more is different)背后的涌现过程的最明显实例。”
——A Career in Theoretical Physics. Philip Anderson.在赫尔曼·外尔(Herman Weyl)1952年的专著《对称》(Symmetry)[1]中,他基于应用于物理领域的数学,总结了一种强有力的现实视角。外尔提出,物理科学最终是一种以对称性分析为基础的探究形式。在物理学中,大量与对称性相关的概念,包括时空对称性、诺特定理、规范对称性和超对称性,这些概念将不变性及其衍生物——普适法则(universal laws),置于对非生命世界的研究核心。这一努力的成功是毋庸置疑的,因为对称性在描述保守动力系统的结构和物质平衡态方面具有重要意义,涵盖了从最大尺度的天体力学,到分子尺度的晶体学点群,再到量子尺度上的酉群(unitary group)。对称性原理(物理定律在各种变换条件下的不变性)及其通过基本对称运动定律的体现,为追求宏大的万物理论提供了基础(在该理论中,宇宙模型是自下而上地组装)。菲利普·安德森(Philip Anderson)的研究源自凝聚态物理,而非粒子及其相互作用。他毕生致力于更广泛的自上而下的流程或构建原则。通过这些原则,微观相互作用最终被其宏观产物所涵盖。1977年,安德森获得诺贝尔物理学奖,以表彰他在磁性和无序体系电子结构的基础理论研究的贡献。安德森关于宇宙宏观结构发展的研究在1972年达到顶峰,他发表了反还原论的物理学涌现宣言,即《多者异也》(More is Different) [2]。在通向“多者异也”的二十年时间里,一直到1980年代和1990年代,安德森试图将复杂现象建立在统计物理学的宏观定律之上。他认知工程(epistemic project)的一部分是促成圣塔菲研究所在1984年成立,他也在论文《通往复杂性理论的八重途径:序章》(The eightfold way to the theory of complexity: a prologue)中总结了自己的动机。这篇文章首次发于1994年[3],标题是对盖尔曼的强子结构八重道分类(Eightfold Way)的致敬。安德森的兴趣在于解释那些不能从物理学基本对称定律中预测的相同结构。他所有工作的基础概念,也可以说是所有复杂现象的基础概念,就是对称性破缺。对称性破缺的后果多种多样,但对于复杂性研究最有意义的是我称之为安德森四原则,它们包括:(i) 通过多样性或缩放引起的涌现性质,(ii) 阻挫随机函数的重要性,(iii) 自主性的要求,以及 (iv) 广义刚性的属性。总的来说,安德森四原则主要是针对平衡宏观态而得出的,它们为我们理解在非平衡状态下通过耗散性或驱动性动力学引发的准平衡结构的涌现提供了必要的基础。这些原则在描述适应性功能方面还存在不足,因为适应性功能超越了任何仅限于平衡结构的理论范畴,但它们应该成为任何此类理论的组成部分。在接下来的部分,我将对这些想法进行总结,并在可能的情况下扩展它们,包括近期发现的结果和现象,以更直接地涉及适应性结构和功能的考虑。对称性破缺:创造超越物理学的空间
安德森在《多者异也》开头引入了对称性破缺的概念,描述了对称物理定律在解释常见的大分子结构时的尺度依赖限制。他选择的例子是氨分子的金字塔结构。氨分子(NH3)被认为具有金字塔状的结构,以每秒大约300亿次的频率在两种状态之间反转或量子隧穿(氨分子涉及的对称性是宇称parity,即空间反演对称)。这个过程的结果是,氨的静态分布是两个相互可逆的金字塔的混合物。氨的两个构型之间的隧穿势垒很低,意味着“一个系统的态,如果是定态的话,其对称性必然与支配它的定律相同”。然而,当考虑稍大一点的分子如磷化氢(PH3)时,反转速率至少慢一个数量级,而三氟化磷(PF3)则更大,反转速率至少再慢一个数量级。当尺度达到生物活性分子,甚至是最简单的碳水化合物的尺度时,宇称对称性的整体概念就崩溃了。分子的静态分布主要由初始条件而不是运动定律所主导。为了解释观察到的结构分布,我们需要一个超越基本定律简约性的解释。超越基本定律描述的附加参数化有效地“计算”了对称性破缺,并通过适当的模型复杂性度量提供了涌现的证据。在最近的一篇综述中,Buhse 等人[4]将这个观点扩展到非平衡状态下的手性分子,并讨论了与手性对称性破缺相关的几种有偏不完美分岔的基本机制。在这种情况下,化学对映体(化学镜像)的混合物被环境手性过程推向稳定的同手性溶液,其中包括流体涡旋和偏振光。在1994年的文章《关于对称性破缺的一些一般性思考》(Some general thoughts about broken symmetry)中[5],安德森对这些主题进行了重要的扩展。在这篇文章中,引入了自主性和广义刚性的概念,我将在后面的部分进行介绍。正如朗道(Landau)关于二级相变理论[6]所描述的那样,在这里,我想简要提到安德森对相变和对称性破缺的强调。众所周知,朗道表明“从晶体向液体或不同对称性的晶体的每个转变,都伴随着某些对称性元素的消失或出现”。对于二级相变(按Ehrenfest的理解),“与物体对称性变化相关的连续相变(就像液体和气体之间的连续相变一样)是绝对不可能的”。安德森将这样的相变描述为朝向更低对称性的运动。例如,凝聚态物质(如某些液晶)中,旋转对称性(各向同性)或平移对称性(均匀性)的消失。对于安德森来说,通过相变改变的物质状态的序参量应被视为对称性破缺程度的度量,而在朗道理论中,这通常是有序性增加的程度。此外,序参量应源自对对称运动定律的理解。通过这种方式,我们可以非常准确地看到基本定律和涌现结构之间的偏离程度。我怀疑1994年的论文无意中造成了许多混淆的陈述,其中涌现和相变被视为同义词。首先,正如安德森迅速指出的那样,他的观点并不适用于所有相变,比如最为人所知的液体到气体的相变,该相变保持了对称性。而对于转变为凝聚态对称性破缺(有序度增加)的相变,正是它们能够支持更多破缺对称(增加无序)的潜力使得它们对生命系统如此重要。正如他在《多者异也》中写道:“尽管晶体是对称的,但它的对称性仍低于完全均匀性”,以及“这种‘载有信息的结晶性’似乎对生命至关重要。”后者当然是对于薛定谔在《生命是什么?》(What is Life?)中关于遗传的非周期晶体猜想的致敬[7]。1. 涌现(性)
涌现的概念可以非常简单地描述为在不损失解释能力的情况下,成功地将物理学基本定理分解出来。安德森将破缺对称作为实现这种效果的主要机制。氨基酸是同手性的,尽管它们的对映异构体出现的概率相等。同样的情况也适用于整个细胞的手性,与原细胞的核酸、蛋白质和碳水化合物领域的自发镜像对称性破缺相关[8]。物理定律无法充分解释这种变异。在更宽泛的组织层次上,这些定律对于肌肉收缩的动作电位编码、Lisp 代码中错误的影响、为什么有些食物尝起来很苦,或者是什么让 Wallace Stevens 的诗行得通等问题,都没有解释力。所有这些都是不同寻常地不受物质基本结构法则支配的现象的候选者。在《多者异也》中,安德森提出了一个包含两列的表格,X列和Y列。在X列中,他列出了遵循Y列科学定律的科学领域的列表。例如,X(化学)遵循Y(多体物理学),X(细胞生物学)遵循Y(分子生物学)。关键在于,“遵循”和“决定”( ‘obey’ and ‘determine’ )并不是同义词。我们可以说,遵循和决定之间的区别是关于对称性破缺数量的陈述。还原论的操作定义是对称性在物理定律中的极限情况,它决定了实证可观测量的分布情况。在还原论下,遵循和决定的含义变得相同。在复杂性研究中,我们追求的是针对感兴趣的量具有决定性解释的有效理论,而这些理论与它们遵循的物理学相差甚远。在某个阶段,对称性对宏观行为变得如此边缘化,以至于甚至对称性破缺的概念也失去了依据。因此,“在某个点上,我们必须停止谈论对称性的减少,开始称之为复杂性的增加。所以随着每个阶段增加的复杂性,我们继续沿着科学的层级结构向前发展”。这不仅仅是累积自由参数的问题,而是发展全新的概念结构。考夫曼(Kauffman)在基因控制回路(或我们现在所称的调控网络)方面的工作是开创性的,他引入了对能够产生稳定分化状态的最小规则系统的关注。在复杂性领域中,涌现规则而不是基本定律体现了复杂性的特点[9]。我发现 Laughlin 等人的工作[10]是对安德森思想的一个非常有说服力的延伸,特别是他们在《中间道路》(The middle way)中对介观尺度组织的阐述。在超越对称性破缺的基础上,他们引入了“受保护状态”(protected states)的概念,这些状态对基本运动方程的微小扰动具有稳定性。因此,“超流性、铁磁性、金属导电性、流体力学等都是物质的‘受保护‘性质——无论细节如何,一个系统与另一个系统可靠地具有相同的一般行为”。以三氟化磷为例,防止隧穿的保护是通过化学势和分子波函数的性质提供的。对于大分子,如DNA的保护是通过复杂而进化的误差修正机制实现的,这些机制被强加在主要的信息传递结构上。生命尺度上的涌现最好是以保护或鲁棒性[11]的机制来考虑,这些机制能够对大幅度扰动进行屏蔽,从而使生物分子及其集合的“有效”运动方程得以调节。通过这些屏蔽机制,例如在疾病监测的情况下,我们就可以用包含四个字母表的大大简化的字符串,以替代原本需要精确描述 RNA 和 DNA 所需的极其复杂的生物学框架。2. 阻挫随机函数
1983年,安德森撰写了一篇相对被忽视的论文《关于生命起源前进化的建议模型:混沌的运用》(Suggested model for prebiotic evolution: the use of chaos)[12]。这篇论文对生命起源并没有提供特别有启示性的信息,但它包含了关于耗散结构理论所面临的挑战的几个重要洞见,并强调了冻结涨落作为适应现象启示的关键作用。耗散结构理论是由普里高津(Prigogine)在1978年的一篇论文《时间、结构和涨落》(Time, structure and fluctuations)[13]中引入的,该论文总结了布鲁塞尔大学过去十年在非平衡热力学领域发展起来的有关生命的新理念。该理论的核心思想是,非平衡结构为生命系统中的原始秩序提供了重要的来源,例如在贝纳德对流中产生的涡旋。普里高津认为,这些规律性现象在玻尔兹曼的平衡秩序原理(Boltzmann’s equilibrium order principle)中是一个盲点。在驱动系统中,相干态(耗散结构)可以自发地涌现,并通过与外界能量交换而稳定下来。这些结构的特点是它们对“表征化学系统环境的全局特征非常敏感,例如大小、形状、对表面施加的边界条件”等等。对于安德森来说,这种敏感性被证明是一个不可逾越的障碍(我将在后面关于自主性和刚性的章节中讨论),即在没有一些机制使平衡结构从动力学中凝聚出来时,无法利用稳态对称性破缺来可靠地储存信息。安德森将这个问题描述为在稳定性需求与多样性要求之间的协调问题。然而,在一个驱动系统中,虽然可能会出现许多耗散结构,但大多数都是短暂存在的,观察到的形式受到其不稳定性的严重限制。问题在于,尽管“可以很容易地建立一个具有稳定结果的过程,但这是以牺牲关键程度的多样性为代价的”。由于稳定性将从大量候选结构中筛选出一个非常小的“可行”集合,因此“混沌是一个先决条件:我们需要一个生存概率,它是分子组成的一个固定但混乱的函数”。安德森认为,从平衡统计力学角度来看,将稳定性与持续的随机源相结合的最有说服力的候选系统是自旋玻璃。这是一个具有自旋哈密顿量的系统,其中具有交换积分Jij 是变量 (i,j) 的随机函数的特殊性质。这种随机性的最直接含义是,由矩阵j定义的图中的循环意味着,并非所有的局部自旋相互作用都可以满足。这就产生了“阻挫随机函数”(frustrated random functions)的概念。由于哈密顿函数的亚稳态解的数目随系统大小呈指数增长,且状态间的弛豫时间非常慢,因此多样性可以与准稳态共存。安德森利用自旋玻璃的阻挫随机函数,定义了一个简单的序列生长、分裂和互补碱基配对模型。在一个相对较弱的随机场的存在下(即对系统自旋状态施加的环境偏置),这个模型能够支持一个多样化的稳定序列集合。自旋玻璃在适应性现象中的另一个更有说服力的应用是由 Hopfield 提出的内容寻址记忆[14]。Hopfield 的重要观察结果显示,由受阻挫随机相互作用提供的简并基态能够存储位序列。因此,系统内在的对称性破缺使其能够存储环境中持久存在的多样性来源。在1987年的论文《自旋玻璃哈密顿量:生物学、统计力学和计算机科学之间的桥梁》(Spin glass Hamiltonians: a bridge between biology, statistical mechanics, and computer science)中[15],安德森强调了哈密顿量在 N→∞ 极限下的相变,即系统打破遍历性,相空间中的不同区域被 N^p (其中 p < 1)阶能量势垒分隔开。自旋玻璃是解决耗散结构尺度依赖敏感性的最简单的平衡系统,它将随机波涨落“冻结”为稳定的凝聚态。这个特性直接导致了所有生命系统的一个基本经验特征,即第三个安德森原则——自主性。3. 自主性
普里高津强调了由小波到平均状态产生的耗散结构的尺度依赖性[13],以及这些波动如何增长到受系统长度限制的幅度。其中许多更有说服力的例子来自流体动力学,包括上述的对流现象,以及气旋、飓风和B-Z振荡反应。最近的研究人员声称所有生命结构都是耗散结构,或者是“生物类耗散结构”(参见[16]进行的最新综述)。尽管这是一个非常有趣的想法,并且无疑是解释适应性形态起源的部分答案,但安德森的敏锐批评不仅仅局限于这一点,他还指出了一种更为微妙和功能上重要的缺陷——缺乏自主性[5]。正如安德森所述,“自主结构的自主性是指其空间或时间结构不应在外部边界条件的尺度上预先确定”。自主性是所有复杂生命形式的重要特征,跳蚤中的细胞不比大象中的细胞更小,呼吸复合物在所有生命形式中的结构和尺度都是相同的,基因的长度不取决于它们所在的细胞或有机体的大小。这个列表可以无限扩展。在简单物理设备(如激光器)以上的尺度上,真正生成“自主的”耗散结构非常困难,因为它们的功能与物理定律相差不远。耗散结构的最初概念出现在艾伦·图灵(Alan Turing)的形态发生理论中[17],除了显示出对域尺寸极度敏感之外,还存在“微调”问题,即稳定的驻波需要对形态生成物的扩散性进行相当精确的调节(参见[18]和[19]中的分析和可能的解决方案)。已经有人尝试将反应扩散系统应用于生物现象,例如鱼皮的条斑形成,但正如研究人员指出的,还需要额外的非耗散性记忆来源来克服由特定参数值引起的固有空间波长[20]。安德森认为耗散动力学在对称性破缺方面起着关键的早期作用,并随后被凝聚成准平衡模式。在形态发生领域,这对应于由涨落驱动的不稳定性产生图灵斑图,然后通过遗传调控网络(长期记忆)在一定延迟后得到巩固[21]。迄今为止,形态发生斑图(pattern)在动力学上具有关键作用。即使耗散结构可以在保持生长敏感性的同时稳定并实现尺度无关,这远远不能满足完整体积斑图发挥任何有用机械工作的要求。这引出了安德森提出的第四个原则——广义刚性。4. 广义刚性
刚性通常被定义为固体在承受机械应力时抵抗形变的能力。詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)在他的论文《论可易图形和力图》(On reciprocal figures and diagrams of forces)中,首先探讨了刚性的重要性,并与力通过一系列刚体的传播有关[22]。几乎我们对经典力学的所有直觉,从台球、弹簧和杠杆,到动物运动,都涉及刚性的概念。毕竟,柔性的零件不能制造可靠的机械钟。安德森对所有刚性相互作用感兴趣,这些相互作用使得控制参数(如温度)能够通过应力系统传递其力量,从而在适当的序参量(如自旋角度)中显现出来。任何非平凡的机制都必须具有广义刚性,且具备以下特点:“(1)......内部自由度不能预先确定;(2)具有可以稳定操纵的自由度,并能够实施远程作用[5]。”尽管刚性对于生物体或机器的运动特征很重要,但对于信息处理同样重要。一个明显的例子是集成电路中的晶体管。晶体管是半导体,通过连接到固定拓扑电路的两个端口传输电流而工作。如果集成电路不能可靠地传输电流,而是具有柔性(在这种情况下泄漏大量电流),计算将无法进行。同样的道理也适用于电化学信号在神经系统中的传播。一个柔性的反射动作只会变成无效的痉挛。我们之所以需要描述连接组(connectome),是因为神经元之间的连接在功能上具有信息性,因为它们揭示了电化学信号的优先传播方式。正如安德森在谈到内部自由度的独立性时所说的,可靠构建刚性系统的关键是自主部件。例如,细胞中的分子马达利用布朗运动的棘轮原理通过刚性相互作用传递力,这涉及通过使用短程吸引力来捕获有利的涨落,从而偏置或整流原本随机的布朗运动。”这些驱动反应向前发展,通过以单体大小的步长进行,利用将单体结合在一起的能量来推动纤维和负载的波动[23]。更基本地说,广义刚性是因果关系的物理先决条件。休谟(Hume)将因果关系定义为可靠的原因和结果,“我们可以将原因定义为跟随着另一个物体,并且所有与第一个物体相似的物体都跟随着与第二个物体相似的物体。换句话说,如果第一个物体不存在,第二个物体就永远不存在。”正如 Halpern 所言[24],刚性使得既有规律性(A然后B)的概念又有反事实(非A然后非B)成为合理的。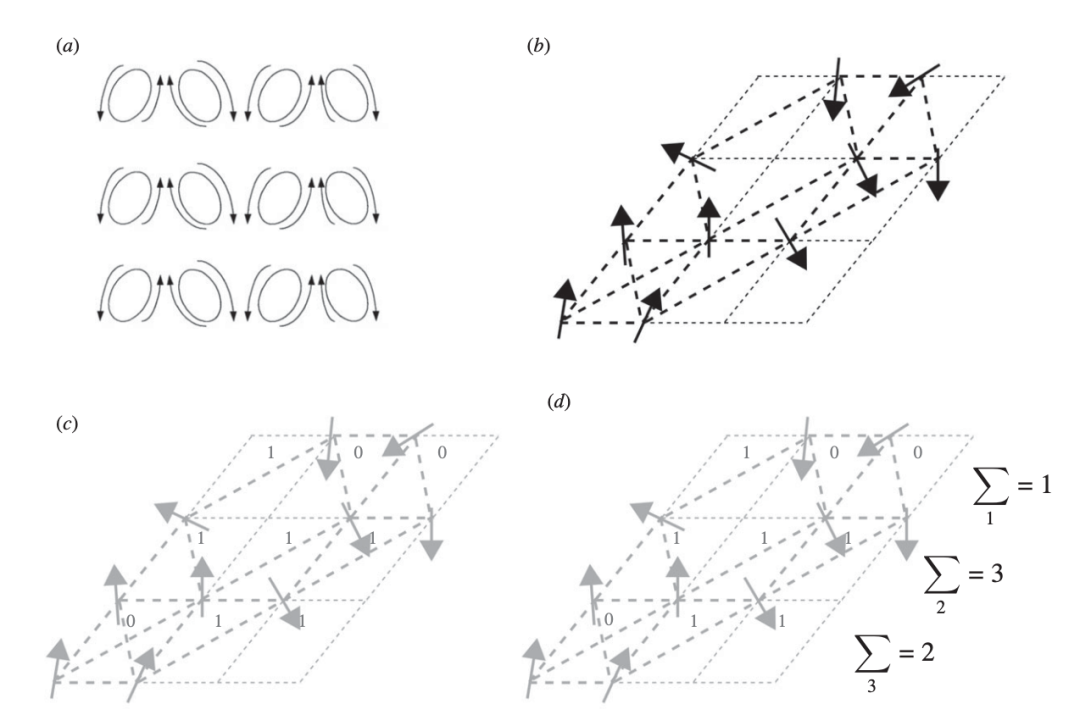
图1 按顺序实现信息处理机制的“安德森四原则”。(a)从一个动力耗散结构开始(例如图灵系统中的扩散驱动的不稳定性),促进不均匀性的斑图形成,具有少量的“自组织”有效维度,这些维度被“冻结”或凝结为一个阻挫的平衡结构(b)(例如形态因子诱导的基因表达持久斑图)。稳定的对称性破缺能够作为信息存储的无序状态存在于“自主”的长度尺度上(c),并用于可靠地传播(例如通过直接序列结合或电化学信号传导)整个结构中的信息(广义刚性),从而执行简单的计算(d)。 ((b-d)修改自https://en.wikipedia.org/wiki/Spin_glass.)
为了说明问题,我给这安德森四原则打上了标签,它们扩展了我们对对称性和对称性破缺在复杂系统中所扮演的关键角色的理解。我发现这些原则是对相变与涌现性、耗散结构与适应性特征,以及斑图形成与机械和计算工作之间关系的许多有疑问的思考的纠正。我有时把它们看作是一个最小的核对清单,以确保任何提出的机制都不仅仅是一个有趣的模式。图1以隐含的顺序说明了这四个原则。安德森没有深入探讨的两个领域是信息论和演化,这两个领域是从他对涌现现象的研究自然延伸来的。信息论可以说是任何测量复杂性的努力中最有效的理论基础(超越简单的对称性破缺),演化则是所有领域中以对称性破缺为基础概念的顶峰——更经常被描述为“冻结的偶然事件”。信息熵毕竟是一种用于计算对称性破缺的计数统计量(在20个问题中的每一个是与否的回答都减少了置换群的基数)。通过突变——漂移——选择的方法来简约重建谱系树,将性状置于根部位置以最小化对称性破缺(Hennig辅助原则)。最大熵方法假设对称性,以便在其身上施加约束或打破对称,这些约束或破缺对称可以通过与数据拟合进行约束[25]。而一般地,复杂性可以看作是与可观测变异一致的最简历史[26]——换句话说,最对称(例如可并行)的过程,可以将随机输入转化为规则输出[27]。
- Weyl H. 1952 Symmetry. Princeton, NJ: Princeton University Press.
- Anderson PW. 1972 More is different. Science177, 393-396. (doi:10.1126/science.177.4047.393)
- Anderson P. 2005 The eightfold way to the theory of complexity: a prologue. In A career in theoretical physics, pp. 779-787. Singapore: World Scientific.
- Buhse T, Cruz JM, Noble-Terán ME, Hochberg D, Ribó JM, Crusats J, Micheau J-C. 2021 Spontaneous deracemizations. Chem. Rev.121, 2147-2229. (doi:10.1021/acs.chemrev.0c00819)
- Anderson PW. 1994 Some general thoughts about broken symmetry. In A career in theoretical physics, pp. 419-429. Singapore: World Scientific.
- Landau L. 1936 The theory of phase transitions. Nature138, 840-841. (doi:10.1038/138840a0)
- Schrödinger E, Penrose R. 2012 What is life? Cambridge, UK: Cambridge University Press.
- Ribó J, Hochberg D. 2019 Chemical basis of biological homochirality during the abiotic evolution stages on earth. Symmetry11, 814.
- Kauffman S. 1974 The large scale structure and dynamics of gene control circuits. J. Theor. Biol.44, 167-190. (doi:10.1016/S0022-5193(74)80037-8)
- Laughlin RB, Pines D, Schmalian J, Stojković BP, Wolynes P. 2000 The middle way. Proc. Natl Acad. Sci. USA97, 32-37. (doi:10.1073/pnas.97.1.32)
- Ay N, Krakauer DC. 2006 Geometric robustness theory and biological networks. Theory Biosci.125. 93-121. PubMed, ISI,
- Anderson PW. 1983 Suggested model for prebiotic evolution: the use of chaos. Proc. Natl Acad. Sci. USA80, 3386-3390. (doi:10.1073/pnas.80.11.3386)
- Prigogine I. 1978 Time, structure, and fluctuations. Science201, 777-785. (doi:10.1126/science.201.4358.777)
- Hopfield JJ. 1982 Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA79, 2554-2558. (doi:10.1073/pnas.79.8.2554)
- Anderson PW. 2018 Spin glass Hamiltonians: a bridge between biology, statistical mechanics and computer science. In Emerging syntheses in science, pp. 17-20. Boca Raton, FL: CRC Press.
- Kondepudi DK, De Bari B, Dixon JA. 2020 Dissipative structures, organisms and evolution. Entropy22, 1305. (doi:10.3390/e22111305)
- Turing A. 1952 The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B237, 37-72. (doi:10.1098/rstb.1952.0012)
- Fuentes MA, Krakauer DC. 2007 The evolution of developmental patterning under genetic duplication constraints. J. R. Soc. Interface5, 237-245. (doi:10.1098/rsif.2007.1074)
- Butler T, Goldenfeld N. 2011 Fluctuation-driven Turing patterns. Phys. Rev. E84, 011112. (doi:10.1103/PhysRevE.84.011112)
- Höfer T, Maini PK. 1996 Turing patterns in fish skin? Nature 380, 678. (doi:10.1038/380678b0)
- Gaffney EA, Monk NAM. 2006 Gene expression time delays and Turing pattern formation systems. Bull. Math. Biol.68, 99-130. (doi:10.1007/s11538-006-9066-z)
- Maxwell JC. 1864 XLV. On reciprocal figures and diagrams of forces. Lond. Edinb. Dublin Philos. Mag. J. Sci.27, 250-261. (doi:10.1080/14786446408643663)
- Oster G. 2002 Brownian ratchets: Darwin’s motors. Nature417, 25-25. (doi:10.1038/417025a)
- Halpern JY. 2017 Actual causality. Cambridge, MA: The MIT Press.
- Jaynes ET. 1957 Information theory and statistical mechanics. Phys. Rev.106, 620-630. (doi:10.1103/PhysRev.106.620)
- Prigogine I. 1987 Exploring complexity. Eur. J. Oper. Res.30, 97-103. (doi:10.1016/0377-2217(87)90085-3)
- Bennett CH. 1988 Logical depth and physical complexity. In The universal Turing machine, a half century survey (ed. Herken R), pp. 227-257. Oxford, UK: Oxford University Press.