
“在12个小球里有一个次品,重量与其他11个球不同。用一个没有砝码的天平,最少称几次,才能保证找到那个次品,并且区分出次品是轻还是重呢?”
我们首先来研究一个简化版本,这是在小学五年级课本上的一道题:“已知有9个球中有一个次品球比其他球更重,用天平至少称几次才能保证找到那个次品球?”相比于标准问题,简化版本多了一个条件——我们知道次品球比其他球更重。这样问题就简单多了,你还记得答案吗?
也许有人说:我可以用二分法,先把球均分成两堆,上天平比较,找到重的一堆,次品就在这里。再把重的一堆均分成两堆,上天平比较…这样,每次就能把球去掉一半,就能最快找到次品啦!其实,二分法并不是步骤最少的。因为天平称一次,有三种状态:左边重、右边重或者平衡。二分法只利用了其中的两种情况。我们应该在每一次测量的时候充分利用天平的特点,减小问题的不确定性,我们大约可以把它称为“三分法”。以9球为例:首先将9个球编号1-9,然后把它们分成均匀的三堆:1、2、3号一堆、4、5、6号一堆、7、8、9号一堆。第一次测量时:把1、2、3号球放在天平左盘,4、5、6号球放在天平右盘,7、8、9号球放在一边。
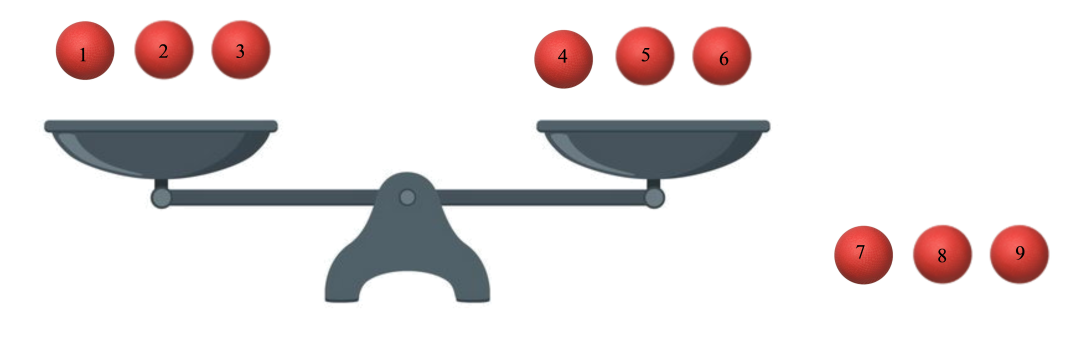
第一次测量
因为次品球更重,所以如果天平向左边倾斜,就说明次品在1、2、3号中;如果向右边倾斜,说明次品在4、5、6号中;如果平衡,说明次品在7、8、9号中。
天平左边重 | 天平右边重 | 天平平衡 |
1号重 2号重 3号重 | 4号重 5号重 6号重 | 7号重 8号重 9号重 |
第一次测量的结果和对应可能
我们发现:无论出现哪一种结果,我都把“从9个球中找次品”的问题转化成“从3个球中找次品”的问题,不确定性大大缩小了。第二次测量时,假设次品在1、2、3号球中,我们就需要再把这三个球再平均分成三份,每一份就只有一个球了。然后,把1号球放在天平左端,2号球放在天平右端,3号球放在一边,进行第二次测量。
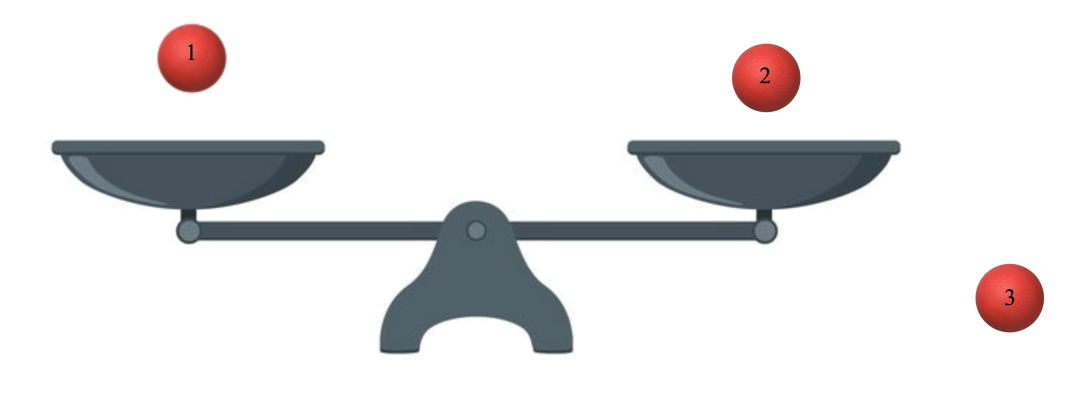
第二次测量
如果天平向左边倾斜,1号球是次品;天平向右侧倾斜,2号是次品;天平平衡,3号是次品。第二次测量,我们把次品的可能范围从3个球压缩到1个球。利用每次均分成3份的方法,我们只需要2次测量,就能从9个球中找到那个较重的次品了。
根据以上的例子,我们发现:如果在已知次品轻重的前提下,想最快找到次品,应该每次将剩余的球均分成三堆,通过天平测量,理想情况下可以把次品的可能性压缩到其中的1/3。假如有N个球,每测一次,次品可能性就被压缩到1/3,测量k次后,次品的可能性小于等于1,我们就保证找到了这个次品。所以,需要满足的条件是:
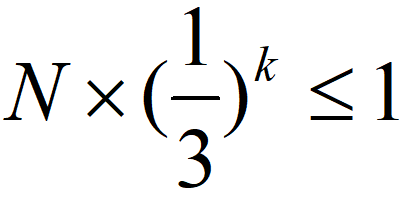
反过来,测量k次,最多能从N个球中找到一个已知轻重的次品球,N必须满足条件:
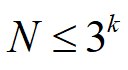
测量次数k | 1 | 2 | 3 | 4 | … |
球的总数N | 1~3 | 4~9 | 10~27 | 28~81 | … |
已知次品轻重时测量次数和小球总数的关系
*注意:如果球的数量不能均分,只需要把不相等的数放在天平下即可。例如有26个球,可以分成9-9-8三堆,9和9上天平,8球在下方,结果不变。消除不确定性,其实是信息熵的作用。大家是否玩过一个游戏,叫做我想你猜。我心里想个人物,你问我问题,我回答是或者否。例如:
每一次是或者否,都能消除一半的不确定度。如果我只认识1024个人,那么你最多问我10个问题,就能猜到我心里想的是谁。同样,在天平称小球的问题中,因为每次有三种可能结果,所以每次消除的不确定性更多。如果问题有是、否、不确定三种回答,理论上10个问题,可以从59049个人物中找到答案。
如果我们只知道次品重量不同,但是不知道是轻是重。至少需要测量多少次,才能保证找到次品,并且测出次品的轻重呢?
显然,如果不知道次品的轻重,那么问题的不确定性就多了。我们还是从简单的情况开始:有6个球,从中找到一个次品,次品的可能性共有12种:1号球轻、2号球轻、3号球轻、4号球轻、5号球轻、6号球轻;1号球重、2号球重、3号球重、4号球重、5号球重、6号球重。第一次测量:将六个球中1、2号放在天平左边,3、4号放在天平右边,5、6号放在旁边。这样分配的原则与之前相同:尽量充分利用平衡的三种可能结果。
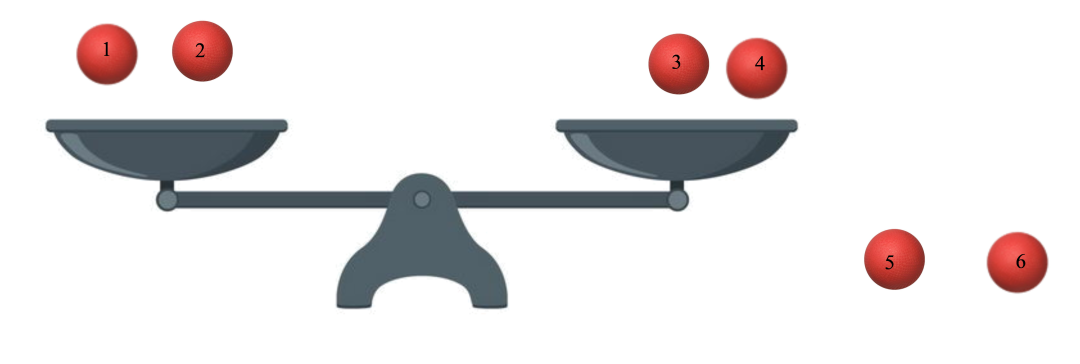
第一次测量
天平左边重 | 天平右边重 | 天平平衡 |
1号球重 2号球重 3号球轻 4号球轻 | 1号球轻 2号球轻 3号球重 4号球重 | 5号球轻 6号球轻 5号球重 6号球重 |
第一次测量结果和对应可能
这样,无论获得什么结果,第一次测量后,我都把12种可能压缩为4种了。
如果第一次测量天平左侧重,我们就知道坏球在1、2、3、4之间,而5和6是好球。第二次测量可以使用这样的策略:1号和3号球放在天平左侧,4号球和一个好球(如5号球)放在天平右侧。

第一次测量左侧重时,第二次测量
根据之间已经获得的信息,容易分析出这时三种结果对应的情况:
天平左侧重 | 天平右侧重 | 天平平衡 |
1号球重、4号球轻 | 3号球轻 | 2号球重 |
第一次左侧重时,第二次测量结果和对应可能
如果第一次测量天平平衡,我们知道坏球在5、6号球中,对应四种可能。此时我们可以用5号球与一个好球(比如1号)比较:

第一次测量平衡时,第二次测量
天平左边重 | 天平右边重 | 天平平衡 |
5号球轻 | 5号球重 | 6号球轻、6号球重 |
第一次测量平衡时,第二次测量结果和对应可能
按照这样的方法,在第二次测量结束后,我们把四种情况压缩到1种或者2种情况之中了。如果只剩下1种情况,那么我们就找到了次品,并且知道了次品的轻重。如果还剩下两种情况,我们只需要让它和好球比一比,就能找到最终答案了。例如:只剩下1号球重和4号球轻两种情况,我们只要拿一个好球和1号球比较就可以了。综上所述:N=6时,我们只需要3次测量,就能保证找到次品,并且知道轻重。
现在我们开始讨论最一般的情况:如果N个球中有一个次品,不知道次品的轻重,那么最初的可能性有2N种。理想情况下,如果每次测量都能将可能性压缩为1/3, 经过k次测量,找到次品球并区分轻重,那么需要满足:
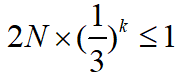
反过来,测量k次最多能从N个球中选出那个不知轻重的次品并区分轻重,N需要满足:
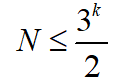
然而,这只是N的上限,受到N为整数的限制,这个上限不一定能取到。假如一共有N个球,其中有一个次品不知轻重,我们测量k次保证能找出这个次品,那么1. 第一次测量:将N个球分为N=a+a+b,天平两边各放上a个球比较
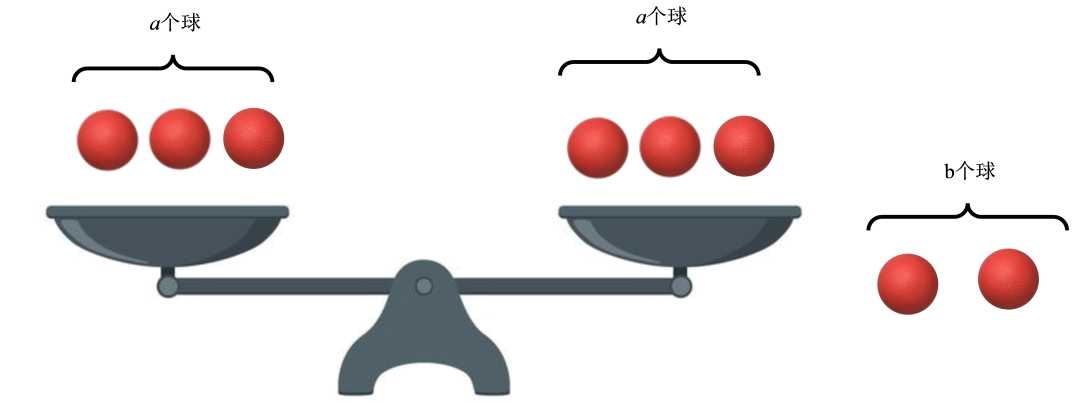
不知次品轻重时第一次测量
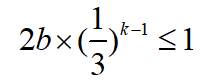
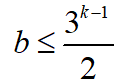
大家注意,右边3k-1是一个奇数,除以2并不能得到整数,但是b必须是整数。所以,这个条件可以进行放缩:
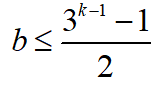
如果天平左边重,说明左侧的a个球中有一个比较重的次品,或者右侧的a个球中有一个比较轻的次品,情况有2a种。再经过k-1次测量,必须找到坏球,所以与刚刚的推导类似,我们依然有:
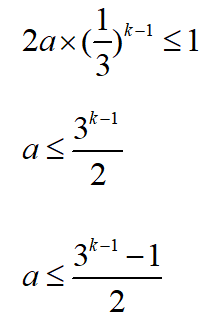
现在我们已经知道了a和b满足的条件,因为N=2a+b,所以这就是测量k次最多能从多少个球中找到那个不知道轻重的次品了。
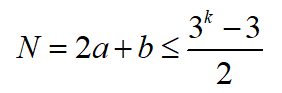
k次测量 | 2 | 3 | 4 | 5 | … |
N个球 | 1~3 | 4~12 | 13~39 | 40~120 | … |
N个球不知次品轻重,需要的测量次数k
从表中很容易找到:如果有12个球,那么3次测量就能找到次品,并且区分出次品的轻重了。
对于这个问题,其实还有许多值得讨论的地方。
例如:我们在讨论出N个不知轻重的球找次品的公式时,进行了一步放缩。为什么只进行一次放缩,而不是测量几次就进行几次放缩呢?
其次,我们现在的问题是:寻找到次品,并且区分次品的轻重。如果我们只想找到这个次品,而不关心它是轻是重,结论又应该是怎样?
还有一个更直接的问题:12个不知道轻重的小球,测量3次就保证找到次品,并且区分轻重,这个结论我们已经得到了。可是,具体通过什么步骤,才能找到这个次品呢?这个问题依然需要耗费一点脑细胞。
对于这几个问题,有想法的同学,欢迎在评论区里留言讨论。