Tiger：一个“抠”到极致的优化器

2023-03-11 10:03

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

这段时间笔者一直在实验《Google新搜出的优化器Lion：效率与效果兼得的“训练狮”》所介绍的 Lion 优化器。之所以对 Lion 饶有兴致，是因为它跟笔者之前的关于理想优化器的一些想法不谋而合，但当时笔者没有调出好的效果，而 Lion 则做好了。

相比标准的 Lion，笔者更感兴趣的是它在时的特殊例子，这里称之为“Tiger”。Tiger 只用到了动量来构建更新量，根据《隐藏在动量中的梯度累积：少更新几步，效果反而更好？》[1] 的结论，此时我们不新增一组参数来“无感”地实现梯度累积！这也意味着在我们有梯度累积需求时，Tiger 已经达到了显存占用的最优解，这也是“Tiger”这个名字的来源（Tight-fisted Optimizer，抠门的优化器，不舍得多花一点显存）。

此外，Tiger 还加入了我们的一些超参数调节经验，以及提出了一个防止模型出现 NaN（尤其是混合精度训练下）的简单策略。我们的初步实验显示，Tiger 的这些改动，能够更加友好地完成模型（尤其是大模型）的训练。

基本形式

Tiger 的更新规则为

相比 Lion，它就是选择了参数；相比 SignSGD [2]，它则是新增了动量和权重衰减。

参考实现：

https://github.com/bojone/tiger

下表对比了 Tiger、Lion 和 AdamW 的更新规则：

可见 Tiger 是三者之中的极简者。

超参设置

尽管 Tiger 已经相当简化，但仍有几个超参数要设置，分别是滑动平均率、学习率以及权重衰减率，下面我们分别讨论这几个参数的选择。

滑动平均率

比较简单的是。我们知道，在基本形式上 Tiger 相当于 Lion 取的特殊情形，那么一个直觉是 Tiger 应当取。在 Lion 的原论文中，对于 CV 任务有，所以我们建议 CV 任务取；而对于 NLP 任务则有，所以我们建议 NLP 任务取。

学习率

对于学习率，Tiger 参考了 Amos、LAMB [3] 等工作，将学习率分两种情况设置。第一种是线性层的 bias 项和 Normalization 的 beta、gamma 参数，这类参数的特点是运算是 element-wise，我们建议学习率选取为全局相对学习率的一半；第二种主要就是线性层的 kernel 矩阵，这类参数的特点是以矩阵的身份去跟向量做矩阵乘法运算，我们建议学习率选取为全局相对学习率乘以参数本身的（Root Mean Square）：

其中

这样设置的好处是我们把参数的尺度分离了出来，使得学习率的调控可以交给一个比较通用的“全局相对学习率” ——大致可以理解为每一步的相对学习幅度，是一个对于模型尺度不是特别敏感的量。

换句话说，我们在 base 版模型上调好的，基本上可以不改动地用到 large 版模型。注意带有下标，所以它包含了整个学习率的 schedule，包括 Wamrup 以及学习率衰减策略等，笔者的设置经验是，至于怎么 Warmup 和衰减，那就是大家根据自己的任务而设了，别人无法代劳。笔者给的 tiger 实现，内置了一个分段线性学习率策略，理论上可以用它模拟任意的。

权重衰减率

最后是权重衰减率，这个 Lion 论文最后一页也给出了一些参考设置，一般来说也就设为常数，笔者常用的是 0.01。特别的是，不建议对前面说的 bias、beta、gamma 这三类参数做权重衰减，或者即便要做，也要低一个数量级以上。因为从先验分布角度来看，权重衰减是参数的高斯先验，跟参数方差是反比关系，而 bias、beta、gamma 的方差显然要比 kernel 矩阵的方差大，所以它们的应该更小。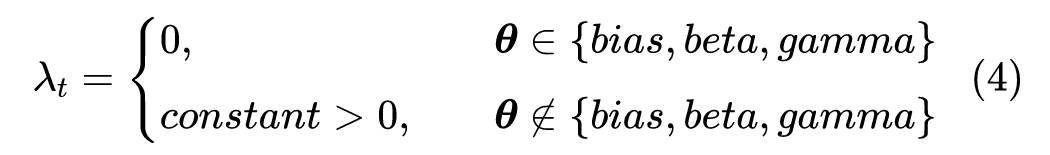

梯度累积

对于很多算力有限的读者来说，通过梯度累积来增大 batch_size 是训练大模型时不可避免的一步。标准的梯度累积需要新增一组参数，用来缓存历史梯度，这意味着在梯度累积的需求下，Adam 新增的参数是 3 组，Lion 是 2 组，而即便是不加动量的 AdaFactor [4] 也有 1.x 组（但说实话 AdaFactor 不加动量，收敛会慢很多，所以考虑速度的话，加一组动量就变为 2.x 组）。

而对于 Tiger 来说，它的更新量只用到了动量和原参数，根据《隐藏在动量中的梯度累积：少更新几步，效果反而更好？》[1]，我们可以通过如下改动，将梯度累积内置在 Tiger 中：

这里的是判断能否被整除的示性函数

可以看到，这仅仅相当于修改了滑动平均率和学习率，几乎不增加显存成本，整个过程是完全“无感”的，这是笔者认为的 Tiger 的最大的魅力。

需要指出的是，尽管 Lion 跟 Tiger 很相似，但是 Lion 并不能做到这一点，因为时，Lion 的更新需要用到动量以及当前批的梯度，这两个量需要用不同的参数缓存，而 Tiger 的更新只用到了动量，因此满足这一点。类似滴，SGDM 优化器也能做到一点，但是它没有操作，这意味着学习率的自适应能力不够好，在 Transformer 等模型上的效果通常不如意（参考《Why are Adaptive Methods Good for Attention Models?》[5]）。

全半精度

对于大模型来说，混合精度训练是另一个常用的“利器”（参考《在 bert4keras 中使用混合精度和 XLA 加速训练》[6]）。混合精度，简单来说就是模型计算部分用半精度的 FP16，模型参数的储存和更新部分用单精度的 FP32。之所以模型参数要用 FP32，是因为担心更新过程中参数的更新量过小，下溢出了 FP16 的表示范围（大致是），导致某些参数长期不更新，模型训练进度慢甚至无法正常训练。

然而，Tiger（Lion 也一样）对更新量做了运算，这使得理论上我们可以全用半精度训练！分析过程并不难。

首先，只要对 Loss 做适当的缩放，那么可以做到梯度不会溢出 FP16 的表示范围；而动量只是梯度的滑动平均，梯度不溢出，它也不会溢出，只能是，更加不会溢出了；之后，我们只需要保证学习率不小于，那么更新量就不会下溢了，事实上我们也不会将学习率调得这么小。因此，Tiger 的整个更新过程都是在 FP16 表示范围内的，因此理论上我们可以直接用全 FP16 精度训练而不用担心溢出问题。

防止NaN

然而，笔者发现对于同样的配置，在 FP32 下训练正常，但切换到混合精度或者半精度后有时会训练失败，具体表现后 Loss 先降后升然后 NaN，这我们之前在《在 bert4keras 中使用混合精度和 XLA 加速训练》[6] 也讨论过。虽然有一些排查改进的方向（比如调节 epsilon 和无穷大的值、缩放 loss 等），但有时候把该排查的都排查了，还会出现这样的情况。

经过调试，笔者发现出现这种情况时，主要是对于某些 batch 梯度变为 NaN，但此时模型的参数和前向计算还是正常的。于是笔者就想了个简单的应对策略：对梯度出现 NaN 时，跳过这一步更新，并且对参数进行轻微收缩，如下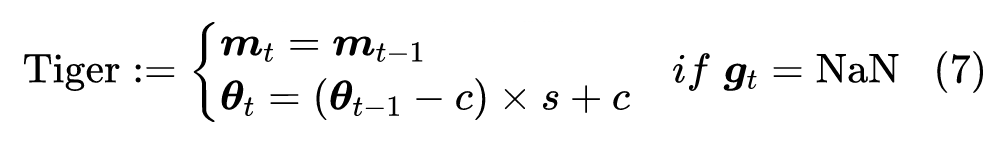

其中代表收缩率，笔者取，则是参数的初始化中心，一般就是 gamma 取 1，其他参数都是 0。经过这样处理后，模型的 loss 会有轻微上升，但一般能够恢复正常训练，不至于从头再来。个人的实验结果显示，这样处理能够缓解一部分 NaN 的问题。

当然，该技巧一般的使用场景是同样配置下 FP32 能够正常训练，并且已经做好了 epsilon、无穷大等混合精度调节，万般无奈之下才不得已使用的。如果模型本身超参数设置有问题（比如学习率过大），连 FP32 都会训练到 NaN，那么就不要指望这个技巧能够解决问题了。此外，有兴趣的读者，还可以尝试改进这个技巧，比如收缩之后可以再加上一点噪声来增加参数的多样性，等等。

实验结果

不考虑梯度累积带来的显存优化，Tiger 就是 Lion 的一个特例，可以预估 Tiger 的最佳效果肯定是不如 Lion 的最佳效果的，那么效果下降的幅度是否在可接受范围内呢？综合到目前为止多方的实验结果，笔者暂时得出的结论是：

也就是说，考虑效果 Lion 最优，考虑显存占用 Tiger 最优（启用梯度累积时），效果上 Tiger 不逊色于 AdamW，所以 Tiger 替代 AdamW 时没有太大问题的。

具体实验结果包括几部分。第一部分实验来自 Lion 的论文《Symbolic Discovery of Optimization Algorithms》[7]，论文中的 Figure 12 对比了 Lion、Tiger、AdamW 在不同尺寸的语言模型上的效果：

▲ Lion、Tiger(Ablation)、AdamW 在语言模型任务上的对比

这里的 Ablation0.95、Ablation0.98，就是 Tiger的分别取 0.95、0.98。可以看到，对于 small级别模型，两个 Tiger 持平 AdamW，而在 middle 和 large 级别上，两个 Tiger 都超过了 AdamW。但正如前面所说，取两者的均值 0.965，有可能还会有进一步的提升。

至于在 CV 任务上，原论文给出了 Table 7：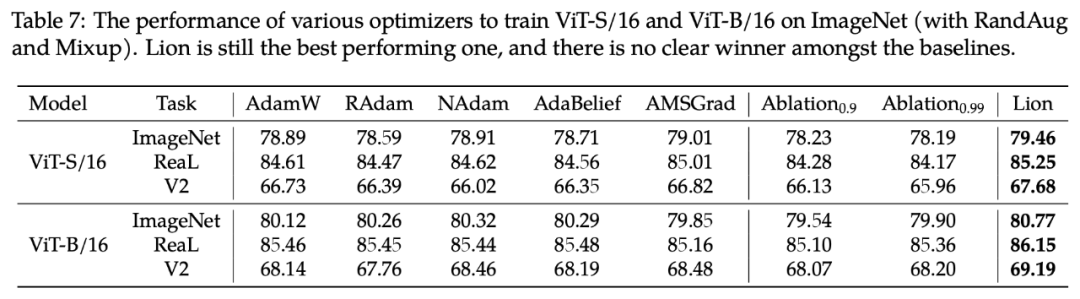

▲ Lion、Tiger(Ablation)、AdamW在图像分类任务上的对比

同样地，这里的 Ablation0.9、Ablation0.99，就是 Tiger 的分别取 0.9、0.99。在这个表中，Tiger 跟 AdamW 有明显差距。但是考虑到作者只实验了 0.9、0.99 两个，而笔者推荐的是，所以笔者跟原作者取得了联系，请他们做了补充实验，他们回复的结果是“ 分别取 0.92、0.95、0.98 时，在 ViT-B/16 上 ImageNet 的结果都是 80.0% 左右”，那么对比上图，就可以确定在精调时，在 CV 任务上 Tiger 应该也可以追平 AdamW 的。

最后是笔者自己的实验。笔者常用的是 LAMB 优化器，它的效果基本跟 AdamW 持平，但相对更稳定，而且对不同的初始化适应性更好，因此笔者更乐意使用 LAMB。特别地，LAMB 的学习率设置可以完全不改动地搬到 Tiger 中。笔者用 Tiger 重新训练了之前的 base 版 GAU-α 模型，训练曲线跟之前的对比如下：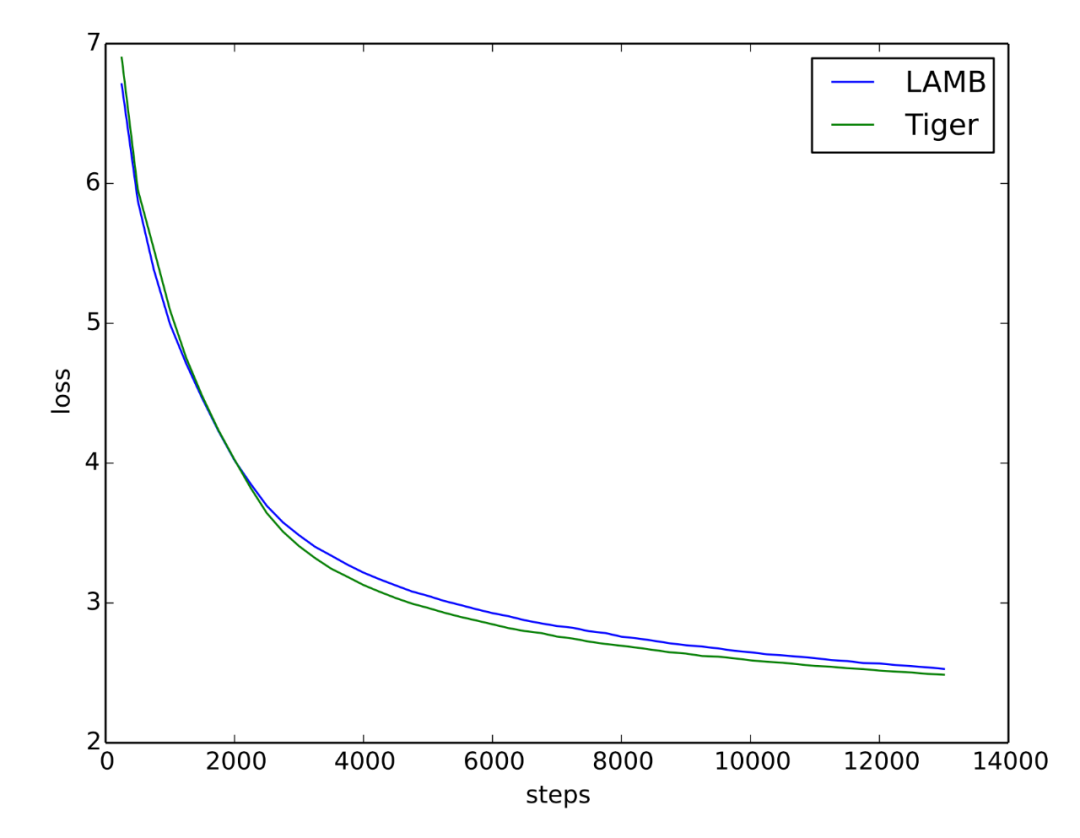

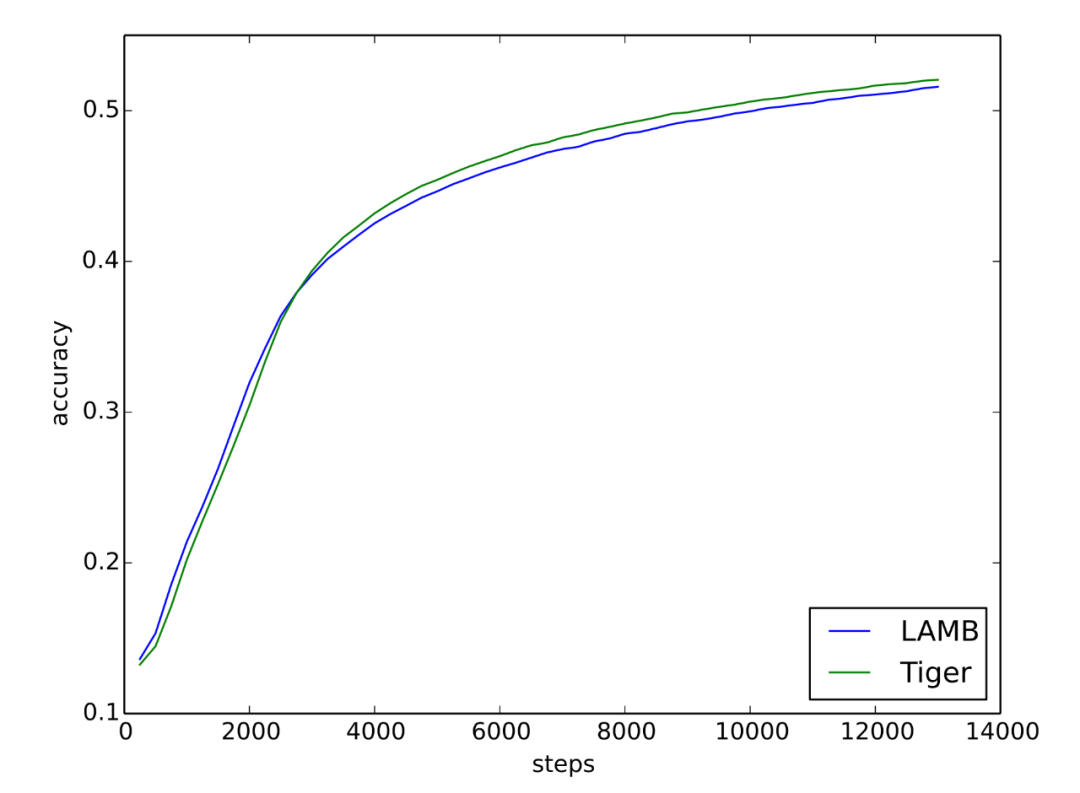
▲ 笔者在GAU-α上的对比实验（loss曲线）

▲ 笔者在GAU-α上的对比实验（accuracy曲线）

可以看到，Tiger 确实可以取得比 LAMB 更优异的表现。

未来工作

Tiger 还有改进空间吗？肯定有，想法其实有很多，但都没来得及一一验证，大家有兴趣的可以帮忙继续做下去。

在《Google新搜出的优化器Lion：效率与效果兼得的“训练狮”》中，笔者对运算的评价是：

Lion 通过操作平等地对待了每一个分量，使得模型充分地发挥了每一个分量的作用，从而有更好的泛化性能。如果是 SGD，那么更新的大小正比于它的梯度，然而有些分量梯度小，可能仅仅是因为它没初始化好，而并非它不重要，所以 Lion 的操作算是为每个参数都提供了“恢复活力”甚至“再创辉煌”的机会。

然而，细思之下就会发现，这里其实有一个改进空间。“平等地对待了每一个分量”在训练的开始阶段是很合理的，它保留了模型尽可能多的可能。然而，如果一个参数长时间的梯度都很小，那么很有可能这个参数真的是“烂泥扶不上墙”，即已经优化到尽头了，这时候如果还是“平等地对待了每一个分量”，那么就对那些梯度依然较大的“上进生”分量不公平了，而且很可能导致模型震荡。

一个符合直觉的想法是，优化器应该随着训练的推进，慢慢从 Tiger 退化为 SGD。为此，我们可以考虑将更新量设置为