让我们把眼光聚焦在局部交易市场的司机和乘客匹配这一核心问题上,该问题作为双边匹配和空间众包方向的学术问题,受到了学术界和工业界的广泛关注。 在滴滴的众多业务之中,存在大量匹配问题,并涉及到各匹配技术领域,例如:
1. 快车、出租车等业务中,涉及单乘客-单司机的双边匹配;
2. 特惠、出租车等业务中,涉及到半指派方式播单,构成单乘客-多司机(可重叠)的双边匹配;
3. 拼车、顺路单等合乘业务中,涉及多乘客-单路途-单司机的多边匹配;
4. 货运等业务中,涉及抢单、派单模式结合的双边匹配方式;
5. 两轮车业务中,涉及乘客-停放站点-车辆的匹配,涉及运维车辆-任务工单的匹配;
6. 国际外卖业务中,涉及订单-骑手-商家的多边匹配,带时间窗口约束;
本文限于篇幅问题,重点介绍最基本的单乘客-单司机的双边匹配问题。 在这个简化问题中:地图上不断有乘客发出新的订单,也存在着等候订单的司机们,派单系统了解他们的位置信息和订单起终点信息,希望将一位乘客分配给一辆空闲网约车,从而完成打车行程。 让我们从最简单的开始,当区域内只有一位乘客开始呼叫,而区域内也只有一名空闲司机,则显然会给该乘客和该司机进行匹配:
复杂一些,当一位乘客开始呼叫,而区域内有多名司机时,则应该为该乘客寻找最优的司机,比如离其最近的司机,或者服务最好的司机:
再复杂一些,当多位乘客都在呼叫,而区域内只有一位司机时,将为该司机匹配更加合适的乘客订单:
更复杂一些,当多位乘客在呼叫,多个司机在听单时,则选择空间成几何倍数增加,平台以公开透明的方式(就近派单原则等)进行最优的匹配:
现实环境之中为了保障司乘的体验,我们还会引入更多的更好的机制来帮助司乘。比如在体育赛事结束后大量乘客一起打车,这时候我们提供乘客的排队功能,“先来后到”,来帮助乘客更公平打车。同样的,在场站等特殊场景,也需要引入司机排队来实现司机师傅的公平接单体验。
运筹学中的双边匹配问题,是指如何在两个不相交的主体集合中依据各主体针对潜在匹配对象给出的偏好信息来确定合适的匹配结果,其在运筹、经济管理领域中存在的广泛应用,并在现实中的拍卖、交易、人员分配等场景得到实际使用。 2012 年的诺贝尔经济学奖颁发给了 Alvin E. Roth 和 Lloyd S. Shapley,以表彰他们在市场设计领域做出的杰出贡献。这项荣誉旨在肯定他们在稳定双边匹配理论及其在实际市场设计中的应用方面所作出的突出贡献。 双边匹配问题的著名起源案例是美国医学界的“毕业生配对”问题:每个医学毕业生心目中有心仪医院的排名,而每个医院考核医学毕业生的标准和门槛各不相同,毕业生希望在尽量更加心仪的医院中实习,而医院也希望招收最合适本院的毕业生,则应当如何匹配? 双边匹配有非常多的算法和优化目标,可以用于实现不同的匹配效果,以满足不同的业务诉求。随着多年来学界和真实场景的不断研究和迭代实验,人们对双边匹配技术有了长足的进步。

滴滴业务场景的部分匹配技术

针对最基本的单乘客-单司机双边匹配场景,我们研究了各类匹配方法,以求更加满足司乘的需求,平衡各方收益。贪心算法(Greedy Algorithm)是当今计算机领域中最基础的算法之一。在双边匹配问题中,贪心算法匹配是一种能够快速、有效地为乘客和司机之间建立连接的算法。它在乘客发出呼叫后,立即寻找最近的匹配司机,以满足该乘客需求。 这种匹配方式虽然简单易行,但是当面对众多乘客同时呼叫时,贪心算法可能缺乏灵活腾挪的空间,使得部分乘客匹配很差的极端情况发生。 图论中的网络流算法是一类数学算法,其中的 KM(Kuhn-Munkres)算法是处理最大化二分图中总匹配权值的一种经典方法。作为匈牙利算法的衍生算法,KM 算法的时间复杂度为 O(n³)。 在使用 KM 算法时,我们需要首先构建一个二分图,将每一个乘客和每一个司机的匹配收益作为权重放入图中。通过设定一个限制条件使得图为二分图,并且通过 KM 算法进行运算,即可获得整体收益最大化的匹配结果。 KM 算法的原理是基于二分图归约和匈牙利算法,其核心是由匹配图和交错树构成的增广路径,步骤包括构造带权二分图、寻找交错树、寻找增广路、更新可行顶标等。在采用最大权匹配的应用中,我们发现,该种匹配方式能够实现定义的某项收益最大化,但并没有充分考虑个体需求,对部分司机和乘客造成了一定的困扰。 因此我们借鉴了 1962 年 David Gale 和 Lloyd Shapley 提出的稳定双边匹配算法——GS 算法(亦称之为延迟接受算法),该种算法根据所有市场主体心目中对交易对手方的青睐程度的排序,最终能够保证“稳定”,而这种稳定的定义则是:不存在这样两个市场主体,他们都更中意对方,而超过他们当前的匹配对象。 有趣的是,Shapley 等人在论文中将其形象地描述为一个没有“遗憾”的相亲匹配场景,即:一帮男子和一帮女子寻找伴侣时,每名男子心目中有对所有女子的排序,同样每名女子心目中有对所有男子的排序,而 GS 算法给出来的最终匹配情况中,不存在某一男子和某一女子相互喜欢程度均大于他们现有匹配对象(显然,他俩更合适),那么就说明所有的婚姻都是“稳定”的,没有“遗憾”。 这也是稳定双边匹配问题被称之为“稳定婚姻问题”(Stable Marriage Problem)的原因。在滴滴网约车场景中,通过该方法可以实现更好的司乘需求满足,避免出现有更希望匹配相互在一起却没有匹配在一起的司乘情况发生:
更进一步,当满足了基本的“稳定”条件后,滴滴可以为司机和乘客做更多,因为稳定匹配不只一个,可以继续“优中选优”。从数学上来说,稳定双边匹配只要满足以下约束条件,而结果是不唯一的:注:M 为司机集合,W 为乘客集合。x 代表最终的匹配结果,1 代表下标表示的两者构成匹配,0 则不构成。A 为所有“可接受对”集合,“可接受对”代表司乘相互可匹配。最后一行公式通过约束限制,保证了无法出现“遗憾”情况,提供了“稳定”性。
“稳定匹配”也并未平台追求的唯一目标,考虑司乘双方的公平性、考虑主体间协同、考虑主观满意度,可以增加更多约束条件和加权优化目标,从而实现不同目标联合的双边匹配目的。在保障了司乘意愿的约束条件下,为实现更加公平、高效、鲁棒、提升司乘整体效率,实现更好的匹配方法,是我们不断探索的方向。在滴滴业务中,存在“半指派”等匹配方式,即一个订单同时向周围多个司机广播,等待有人抢单。这种匹配需求需要一次性将多个司机匹配上同一个订单,而非先前的一对一匹配。 为了更好地满足此类情况下的匹配需求,我们采用并改进了稳定双边匹配的一对多算法“医院/居民问题”(The Hospitals / Residents Problem)。该算法可有效应对多个需求方和供应方之间的匹配问题,通过建立数学模型,将订单和司机之间的匹配问题转化为医院和居民之间的问题,从而实现更高效、稳定的双边匹配。 再比如,滴滴拼车业务场景之中,可由多名顺路乘客“拼”到一辆车,即一辆车可能同时匹配上多名乘客,这同样构成一对多的匹配问题。值得思考的是,在该种场景下,如何考量可拼关系?司机、乘客的利益如何评价?社会总效用如何定义和最优化?
值得一提的是,21 世纪以来,我国学者基于一对多双边匹配算法,针对性研究高考录取问题,将我国高考传统录取采用的波士顿机制,升级为平行志愿填报方式,给予考生和高校更好的录取匹配结果,减少“录取遗憾”的发生。平行志愿算法相比起波士顿机制提供了更高的稳定性,但受限于客观条件,还达不到 GS 算法的稳定程度。 类似的,滴滴在面临多种多样的出行场景下,努力升级算法,解决各类交易规则下的技术难题,以司机和乘客利益为中心,提供更加稳定、更加贴心的匹配分单结果。 以上例子仅为滴滴最常见场景下的基础双边匹配问题,由于在多种多样的出行服务业务和场景之中存在复杂而多变的双边匹配情况,限于篇幅,不再过多展开。 在之前所提到的算法中,大多数算法都依赖于司机对乘客的挑选偏好以及乘客对司机的挑选偏好,滴滴作为中立平台,需要充分考虑司乘双方意愿,使得双方获得最满意的体验。
这一部分的设计中,我们会综合考虑路况、时间等因素,并结合机器学习模型的建模和预测,海量的历史数据和先进的算法技术,以实现对乘客和司机的更好预测。此外,对于乘客和司机的走访调研也是至关重要的,通过收集他们的反馈和建议,不断优化匹配算法,提高匹配效率,同时也保证了他们的出行体验。落实在双边匹配技术方面,不同于传统的“完全偏好序”信息,也有针对不完全偏好序、模糊偏好序、区间偏好序等的匹配方法,可以支持多种多样的司乘相互偏好计算,提供匹配落地方法。
相较于前文所提到的双边匹配,网约车的现实问题变得更加复杂。这是因为在网约车的场景下,叫车需求是一个动态的过程,而司机也并不是像传统的货物配送服务那样全天都在为一个订单服务。这种复杂性需要进一步抽象为一个“动态双边匹配问题”。这个问题的解决需要考虑到在全天时间流动的过程中,会不断出现新的订单并持续一段时间,同时也会不断出现有空闲时间的司机,而这些司机在接单后也需要一定的时间才能再次接单。在这个情境下,平台需要做出更好的匹配,从而实现整体的收益最大化,同时也使得司机和乘客都更加满意。为了解决这个问题,平台可以采用动态规划、近似算法等技术手段,对这个问题进行建模并设计相应的算法。在算法的设计中,需要考虑到乘客和司机的空闲时间、收益、服务时间等多种因素,并将这些因素统一纳入到一个优化目标中。同时,为了使算法更加可行和实用,平台也需要结合实际情况对算法进行实时优化和调整,以满足用户需求和市场变化。
动态双边匹配的一种简化解法是最优停止问题(Optimal Stopping,也称之为秘书问题),在该问题的原始版本描述中,描述如下:公司要聘请一名秘书,共有 n 个应聘者,每次面试一人,面试官总能将其与之前所有应聘者比较,面试后立即决定是否雇佣他,如果决定不雇佣,则无法未来挽回。这种情况下应该怎么决策,能够使得选中最佳人选的概率最大?在上述的原始秘书问题之中,科学家找出来的最优策略是:先观测前 1/e 比例的秘书,在剩下的秘书面试之中,当遇到比前面更好的秘书,就作为最终选择。 在滴滴网约车场景中,涉及到的是对司机和乘客双方同时进行的“最优停止”决策,则问题更加复杂。同时,近年机器学习兴起后,对最优停止问题进行“有未来预估”的更优化决策,可根据预测准确率的不同,来尽可能逼近最优解。
2.2.3 基于强化学习决策的动态双边匹配
动态双边匹配问题本质上是一个序列决策问题,需要采用高效、准确的算法进行解决。强化学习作为一种基于试错学习的算法,可以非常好地应用于动态双边匹配方向的研究中,因为它能够通过与环境交互不断地试验和调整策略,从而逐步提升匹配效率和质量。这也是动态双边匹配方向从过去的确定性算法转向探索性算法的重要原因之一。 在强化学习的研究中,我们利用强大的仿真系统作为 Environment ,将匹配操作抽象为可行的 Action ,并以整体双边实体局面作为 State,从而探索出了多条强化学习研究路线。这些研究路线不仅考虑了匹配效率的优化,还包括了对于匹配过程中出现的不确定性和变化的适应性,这为我们更加全面地理解和应用强化学习算法提供了有力支持。在动态双边匹配环境中,司机和乘客之间的价值判断需要更加细致和全面。这是因为这种环境下,价值的判断不仅基于现有的可见、可匹配对象,还需要预测未来可能出现的情况,例如:为乘客估计可能出现更近的空闲司机,从而更快接驾。这种复杂的未来价值预估问题需要利用更为复杂的历史经验数据和未来趋势进行分析,然后将分析结果融入到动态双边匹配决策行为之中,才能够解决这些问题。
作为共享出行平台,滴滴充分利用共享带来的多赢局面,帮助司机规划路线和构建合乘订单,提高了出行效率,降低了出行成本。在拼车业务中,滴滴将多个路线接近但又不同的订单拼在一起,一次性满足乘客的需求,从而提高了车辆的载客率和出行效率。然而,拼车带来的路程增长和不完全顺路等问题,也需要乘客和司机适当承担。平台需要通过合理的定价机制,让司机和乘客受益于拼单,同时保证合理的路程和费用。对于新手司机而言,没有足够的做单经验,可能会导致收入不稳定。滴滴平台提供辅助规划路线的服务,将可能的一系列订单串起来提供给司机,提升了司机的收入。平台还可以通过数据分析和智能算法,优化路线规划,帮助司机更好地完成订单,并提高司机的服务质量和用户体验。PDP/VRP 问题是传统运筹学方向的经典问题,其中种类和延展非常多:
1. PDP 问题(Pickup and Delivery Problems)泛指所有运送问题
2. VRP 问题(Vehicle Routing Problems)则更偏向车队运输路径规划问题
3. 静态 VRP 问题偏向于提前知道全天的货物和车辆信息,从而预先规划好所有路线
4. 动态 VRP 问题偏向于货物和车辆的信息随时动态变化,从而随时调整规划路线
5. 带时间窗口的 VRP 问题,增加了运输时间点的限制
6. 带容量限制的 VRP 问题,限制了车辆同一时间可运输的总货物量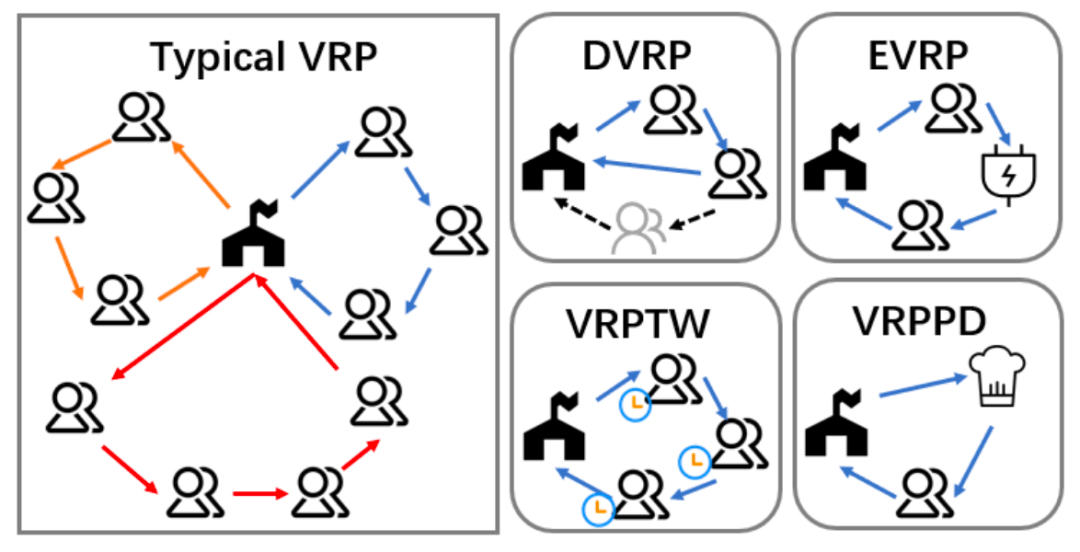
图片来自:Zong, Z., Feng, T., Xia, T., Jin, D. & Li, Y. Deep Reinforcement Learning for Demand Driven Services in Logistics and Transportation Systems: A Survey. Preprint at https://doi.org/10.48550/arXiv.2108.04462 (2022).在预约制的品类中,我们可以提前获取客户在全天内的订单需求和可用车辆情况,进而制定全天车队路线,从而提高出行效率。这种预约制的服务模式不仅能够为乘客提供更加便捷、可靠的出行服务,也能为司机提供更加稳定的收入来源,是一种互利共赢的商业模式。当然,现实之中还可能出现各种意外,我们也要为意外提供可预见的兜底服务。在拼车业务中,我们采用路径订单规划和双边匹配算法,旨在为乘客提供更加经济、便捷的出行服务。我们通过对订单需求进行分析,将起点和终点相近的订单匹配在一起,尽量提供顺路拼乘的服务,同时也能够最大限度地减少车辆空驶的情况,提高车辆利用率,在此基础上实现双边匹配的最优化。在更复杂的场景,例如设置中转站、小巴换乘、地铁公交联乘等情况下,则加入了更复杂的链路限制,对路径订单规划提出了更高的挑战。
打车排队是运力严重不足时保证乘客确定性的重要能力,能够给予乘客公平的感知和耐心等候的保障,在极端条件下仍能够尽力满足乘客需求。 然而在上述传统匹配技术并没有充分考虑排队匹配问题,排队体验并没有得到充分保障。 我们引入排队论,并通过数据分析,将网约车排队场景刻画为多个独立的 M/M/1 排队问题。(在排队论中,“M/M/1 排队问题”指的是:新来订单入队分布符合泊松过程分布,即间隔时间符合负指数分布,服务时间符合负指数分布,单服务台模型。) 根据排队论可以研究稳态状况下的各类队列事件、队列长度的概率情况,也可以采用模拟方法进行瞬态分析,掌握队列的动态变化情况,从而为进一步决策提供信息。为验证真实情况是否满足以上数学抽象,我们进行了滴滴真实排队情况的随机过程研究:
【北京某日排队入队间隔的假设检验结果】
原假设:队列入队间隔分布与负指数分布一致
检验结果:
Kolmogorov-Smirnov检验:pvalue=0.45 >= 0.05
Wilcoxon检验:pvalue=0.41 >= 0.05
Kruskal-Wallis检验:pvalue=0.09 >= 0.05
结论:原假设成立,即【队列入队间隔分布服从负指数分布】
针对相邻的不同地图队列间运力严重不均衡的问题,我们挖掘了经典场景,发现存在资源错配,例如下图中:个别区域队列人数非常多,而周边空闲运力没有及时补充到该地区,从而影响乘客体验,存在供需错配。
进一步的,可以将问题抽象为资源分配(Resource Allocation)问题,借鉴其他领域的技术方案(例如控制领域多智能体系统一致性控制、卫星频段带宽流控),采用模型构建公平、平衡的运力协调方法,最终保证队列双边匹配的体验。

在面对复杂业务决策中,由于现实环境的试验成本过高或者干扰因素过多,我们会转而求助于高精度的数字孪生仿真系统,从而获得成本更低、精度更高的决策数据。滴滴算法团队与工程团队密切合作,构建了完整的交易模拟系统,从而能够在虚拟环境中构建完整的市场环境运行。进一步的,在虚拟环境中验证不同策略对交易市场产生的影响,寻找市场效率理论上限,实现对真实环境的策略优化。当拥有了这一工具之后,不仅可以手工进行策略优化仿真验证,还可以直接利用强化学习从仿真环境中学习,再尝试迁移到现实环境之中。
基于完整的仿真系统,我们针对司乘匹配进行了上限探索,并给出了不同已知信息的情况下,能够实现的效率上限。在在线算法技术领域,将某个策略下的效率与完全最优信息策略下的最优效率的比值,称之为“竞争比”(competitive ratio)。 通过我们的仿真分析,得出了某一场景下的已知信息竞争比情况,提供了对分单未来发展的重要方向论证,在某一个场景下的不同预知信息情况下的竞争比如下:

总结
当今交易市场的复杂性越来越高,市场决策所面临的挑战也随之增加。在这种多方参与的出行环境中,在坚持“就近派单”的基本原则之下,兼顾口碑值、司乘体验等因素都会对交易决策产生影响。同时,市场还充满了各种未知因素和意外情况,如突发天气、未知需求等,这些都使得交易决策变得更加困难。为了在如此复杂的环境下提升效率,滴滴交易策略不断探索新的技术和策略,通过对交易市场的深入分析和对用户需求的充分理解,最终将技术服务于业务,滴滴在双边市场策略优化方面取得了显著成果。在司乘匹配方向,滴滴不断研究最优匹配算法、司乘价值评估、路径订单规划和仿真等多方面的技术,以实现更高效、更智能、更优质的司乘体验。为了将这些技术落地实现,滴滴也构建了完整的迭代框架,将技术与业务相结合,形成了全套解决方案。希望以上内容能够为您了解交易市场及其交易策略提供帮助,敬请期待下期内容。
1. Alonso-Mora, J., Samaranayake, S., Wallar, A., Frazzoli, E., and Rus, D.: On-demand high-capacity ride-sharing via dynamic trip-vehicle assignment, Proceedings of the National Academy of Sciences, Vol. 114, No. 3, pp. 462–467 (2017)
2. Tong, Y., Zhou, Z., Zeng, Y., Chen, L. & Shahabi, C. Spatial crowdsourcing: a survey. The VLDB Journal 29, 217–250 (2020).
3. Roth, A. E. & Sotomayor, M. Chapter 16 Two-sided matching. in Handbook of Game Theory with Economic Applications vol. 1 485–541 (Elsevier, 1992).
4. Mehta, A. Online Matching and Ad Allocation. TCS 8, 265–368 (2013).
5. Antoniadis, A., Gouleakis, T., Kleer, P. & Kolev, P. Secretary and Online Matching Problems with Machine Learned Advice. in Advances in Neural Information Processing Systems vol. 33 7933–7944 (Curran Associates, Inc., 2020).
6. Boysen, N., Briskorn, D. & Schwerdfeger, S. Matching supply and demand in a sharing economy: Classification, computational complexity, and application. European Journal of Operational Research 278, 578–595 (2019).
7. Pillac, V., Guéret, C. & Medaglia, A. Dynamic Vehicle Routing Problems: State of the art and Prospects. Preprint at https://hal.archives-ouvertes.fr/hal-00623474 (2011).
8. Zong, Z., Feng, T., Xia, T., Jin, D. & Li, Y. Deep Reinforcement Learning for Demand Driven Services in Logistics and Transportation Systems: A Survey. Preprint at https://doi.org/10.48550/arXiv.2108.04462 (2022).
本篇文章作者仲晨,来自滴滴网约车 MPT 团队(Marketplace Technology)。团队致力于打造世界顶尖的智能交易平台,包括订单分配、司机调度、拼车、定价、补贴等方向,通过不断探索机器学习、强化学习等前沿技术,完善交易市场设计,实现资源最优化分配,力求解决正在发生的以及潜在供需失衡的状况,最大程度满足平台多样化的出行需求,持续优化乘客体验和保障司机收入,提升业务经营效率,引领出行行业变革与发展。
岗位职责:
1. 负责核心的派单引擎架构的设计与开发,分布式匹配计算系统等;
2. 负责分单,导流、供需预测等复杂策略的架构设计和开发;
3. 负责新业务模式的探索。
岗位职责:
1. 研究包括独乘、拼乘模式下的各种交易匹配、分单调度、乘客预期等算法,持续提升核心交易效率;
2. 利用因果推断、运筹规划、机器学习等技术,提升供需预测、补贴定价等运营核心算法效果;
3. 利用算法技术实现集团各业务线用户的高效增长,优化流量运营效率;
4. 通过机器学习技术解决司乘纠纷和体验问题,打造良好司乘体验和平台秩序,构建司乘公平的判责能力,守护司乘的安全。
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
