从梯度最大化看Attention的Scale操作

2023-11-13 05:11

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 月之暗面

研究方向 | NLP、神经网络

我们知道，Scaled-Dot Product Attention 的 Scale 因子是，其中是的维度。这个 Scale 因子的一般解释是：如果不除以，那么初始的 Attention 就会很接近 one hot 分布，这会造成梯度消失，导致模型训练不起来。然而，可以证明的是，当 Scale 等于 0 时同样也会有梯度消失问题，这也就是说 Scale 太大太小都不行。

那么多大的 Scale 才适合呢？是最佳的 Scale 了吗？本文试图从梯度角度来回答这个问题。

已有结果

在《浅谈Transformer的初始化、参数化与标准化》[1] 中，我们已经推导过标准的 Scale 因子，推导的思路很简单，假设初始阶段都采样自“均值为 0、方差为 1”的分布，那么可以算得

于是我们将除以，将 Attention Score 的方差变为 1。也就是说，之前的推导纯粹是基于“均值为 0、方差为 1” 就会更好的信仰来得到的结果，但没有解释让 Attention Score 的方差为 1，也没有评估是否真的就解决了梯度消失问题。

当然，从已有的实验来看，至少一定程度上是缓解了这个问题，但这毕竟是实验结果，我们还是希望能从理论上知道“一定程度”究竟是多少。

计算梯度

既然涉及到了梯度，那么最好的办法就是把梯度算出来，然后定一个优化目标。设

是归一化因子，那么可以直接算得：

或者可以简写成

。很明显，当时梯度为 0；当时，之中只有一个 1、其余都是 0（假设中只有唯一的最大值），梯度也是 0。

为了更有利于优化，我们应该选取使得梯度尽可能最大化。为此，我们以L1范数作为梯度大小的度量：

从最后的结果不难猜到，之所以选择 L1 而不是其他的根本原因是因为 L1 范数的计算结果足够简单。值得指出的是，这里出现了，它本质上就是我们在《如何度量数据的稀疏程度？》介绍过的 “Rényi 熵”，跟信息熵类似，它也是不确定性的一种度量。

有了优化目标后，我们就可以着手进行最大化了。注意的定义里边也包含，所以这是一个关于复杂的非线性目标，看上去求解析解是不可能的，但我们可以针对一些特殊例子求近似解。

正态分布

首先，我们可以接着前面的结果来做，当我们通过除以使得 Attention Score 的均值为 0、方差为 1 后，我们就可以近似假设，然后再求的最优解，如果，那么就意味着原来的就是最优的 Scale 比例了，否则才是最佳的 Scale 比例。

我们用期望去估计求和

对于服从标准正态分布的，我们有

代入上式，然后代入式（3），得到

最后的近似，虽然已经足够简化了，但其实也不容易求出最大值来。不过无妨，我们可以遍历一些，然后数值求解出取最大值时的，这样我们就大致能看到与的关系了，Mathematica 的参考代码如下：

 1(*定义函数*)
 2f[a_, n_] := a*(1 - Exp[a^2]/n)
 3(*找到函数的最大点对应的a*)
 4FindArg[n_] := 
 5 Module[{a}, a = a /. Last@NMaximize[{f[a, n], a > 0}, a][[2]]; a]
 6(*给定n的范围*)
 7nRange = 40*Range[1, 500];
 8(*求出每个n对应的a*)
 9args = FindArg /@ nRange;
10(*画出a与n的函数图像*)
11ListLinePlot[{args, 0.84*Log[nRange]^0.5}, 
12 DataRange -> {40, 20000}, AxesLabel -> {"n", "a"}, 
13 PlotLegends -> {Row[{"a", Superscript["", "*"]}], 
14   TraditionalForm[HoldForm[0.84*Sqrt[Log[n]]]]}]

经过拟合，笔者发现一定范围内最优点与大致满足的关系，所以也已经将对应的近似函数一并画在一起：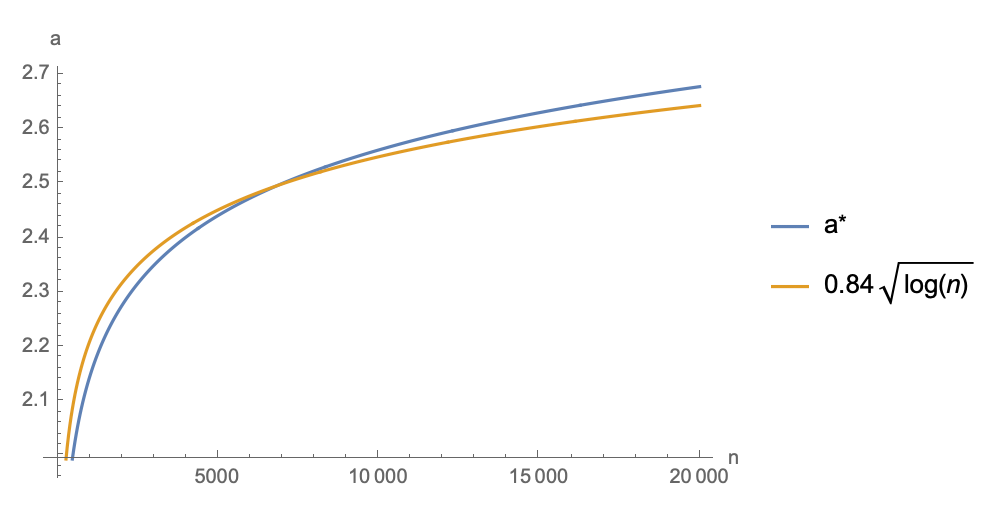

▲ 标准正态分布的最优 alpha 与 n 关系

可以看到，在相当大的一个范围内，的最优值都在之间，所以折中一下的话，盲取作为 Attention 的 Scale 因子理论上更有利于优化。

余弦分布

现在我们考虑另一个不那么常见的例子：当我们对都做归一化变成单位向量后，它们的内积就变成了夹角余弦，即近似服从维空间中的两个随机向量的夹角余弦分布。这个分布可能有些读者并不熟悉，但之前我们在《n维空间下两个随机向量的夹角分布》[2] 已经探讨过，它的概率密度具有形式

看上去并不复杂，但事实上这个形式比正态分布难处理得多，主要是已经不像式（5）那样可以用初等函数表达出来了，不过对于 Mathematica 数值求解数值求解来说问题不大。跟上一节同样的思路，近似式（4）也同样适用，先数值求解最大值，然后再拟合，结果如下（图中，跟相关）：

▲ 余弦分布的最优 alpha 与 n 关系

可以看到，与拟合得也不错（换一个的话，3.5 这个系数会变化）。可以看到，在一个相当大的范围内，都是之间，所以如果用值作为 Attention Score 的话，就需要乘以一个之间的 Scale，才能使得模型比较容易训下去。这同时也解释了为什么我们在用值构建 Softmax 分布（比如 AM-Softmax、SimCSE [3] 等）时，需要在之后乘上一个 30 左右的 Scale 了，因为不乘是很难训得动模型的。

对于不同的和，读者可以自行修改下面的代码计算最优：

 1(*定义函数*)
 2h[a_] := 
 3 Integrate[Exp[a*s]*(1 - s^2)^((d - 3)/2), {s, -1, 1}, 
 4  Assumptions -> {d > 10}]
 5g[a_] = h[a]/h[0] // FullSimplify;
 6f[a_, n_] := a (1 - g[2*a]/g[a]^2/n) /. {d -> 128}
 7(*找到函数的最大点对应的a*)
 8FindArg[n_] := 
 9 Module[{a}, a = a /. Last@NMaximize[{f[a, n], a > 0}, a][[2]]; a]
10(*给定n的范围*)
11nRange = 40*Range[1, 500];
12(*求出每个n对应的a*)
13args = FindArg /@ nRange;
14(*画出a与n的函数图像*)
15ListLinePlot[{args, 3.5*Log[nRange]}, 
16 DataRange -> {40, 20000}, AxesLabel -> {"n", "a"}, 
17 PlotLegends -> {Row[{"a", Superscript["", "*"]}], 
18   TraditionalForm[HoldForm[3.5*Log[n]]]}]

相关思考

本文的标题和结果，尤其是余弦分布中近似正比于的结果，很容易让我们联想到另一篇讨论 Attention Scale 的文章《从熵不变性看Attention的Scale操作》。

事实上，两篇文章的联系确实存在，本文的优化目标（3）出现了 “Rényi 熵”，而“熵不变性”的熵指的是香侬信息熵，两者的性质很大程度上是一致的。最大化式（3）使得它进入了一个“缓变”的区域，这意味着 “Rényi 熵” 关于的变化是很慢的，也意味着信息熵关于关于的变化是很慢的，这就约等于熵不变性。

此外，对于双向 Attention（Encoder）来说，假设训练样本长度相同，那么就是一个常数，我们可以根据算得相应的最优，然后固定在模型中即可；但是对于单向 Attention（Decoder）来说，每个 token 的实际上都不一样（位置 id 加 1），所以理论上无法做到对所有 token 都最大化式（3），不过由于关于的变化较慢，所以取一个差不多的值就行了，比如可以取，这样对大部分 token 的梯度都比较友好了。

文章小结

本文从梯度的角度探讨了 Attention Scale 因子的选择问题。众所周知，关于这个 Scale 因子的“标准答案”是，但其推导过程中并没有讨论到它的最优性问题，所以笔者定义了一个 Softmax 梯度的优化目标，从最大化该目标的角度探讨了 Scale 因子的最优值。相关结果既可以用来改进 Attention 的 Scale 因子，也可以用来解释相似度的对比学习的温度参数。