海归学者发起的公益学术平台
分享信息,整合资源
交流学术,偶尔风月

编者按:应读者的要求,知社重发动力学平均场三十年发展史的系列文章,敬请关注!
动力学平均场对动量和能量空间的分离,使得我们有额外的精力去考虑更为真实的电子环境,比如固体中的电子行为。在固体中电子的运动一方面受到晶格周期性势场的影响,遵从布洛赫定理;另一方面又受到原子空间排列导致的对称性的影响,会表现出比孤立原子周围电子更为丰富的物理特性。这一系列中我们聊一聊其中的多轨道效应。多轨道的出现使得电子在不同轨道间的分布出现了更多的可能性,因此带来了更丰富的物理。这是我们在有了动力学平均场的简化后才有心思去琢磨的有趣问题。
人们最早是在单轨道(能带)中理解电子关联驱动的金属绝缘体转变的。它的图像相对简单,构成了我们今天要聊的更为复杂的金属绝缘体转变的基础。实际材料中的相互作用通常都很复杂,各种宏观物理现象背后的微观机制并非单一来源。在今天的这个系列中,我们只关心由电子-电子关联导致的莫特金属绝缘体转变,至于材料空间群的改变、集体凝聚(例如电荷密度波,自旋密度波,超导等)、磁性长程有序等其他机制,不在我们的讨论范围内。

图片来自于电影《我的野蛮女友》截图,如涉版权问题,将立即撤换
作为准备知识,我们首先简单回顾一下最简单的单轨道体系中的莫特转变。我们曾在系列二中介绍过莫特转变,已经了解到它是不同于传统能带填充的一种新型的金属绝缘体转变机制。莫特转变的前提条件是能带/轨道是刚好一半填充的,平均而言,每个态上都占据了一个电子。由于电子携带有自旋,每个态上最多允许同时被自旋向上和向下两个电子占据。因此,我们称平均每个态上被占据了一个电子的情形为电子半填充。对于每个态而言,都只是被占据了一部分状态,因此电子可以流动起来,从一个地方跑到另外一个地方的未占据状态。从传统能带填充角度理解,这样的系统应该是一个金属。然而,如果我们考虑了同时占据在同一个空间格点的两个自旋相反电子之间的强库仑排斥力,那么所有的电子都倾向于老老实实的待在自己的位置上不流动。因为虽然别的地方上存在一个空态,原则上可以让其他电子流动到那里,但是一旦占据了这个态,就会和原来已经处在该格点上的相反自旋电子形成双占据态,他们之间就会感受到强烈的库仑排斥力,使得系统整体的能量提升,这是在量子力学中一件不划算的事情,因此发生的概率很小。
做个不恰当的比喻,这个过程就好像是两个恋爱中的年轻人,当长辈不在身边的时候,他们可以自由的牵手,表达爱意。两个年轻人就是分别携带相反自旋的两个电子,如果忽略电子间的库仑排斥,他们可以自由跑到对方的位置上。但是当长辈(电子间强库仑排斥力)出现了,两个年轻人不得不表现得更矜持、有礼貌些,因此他们只能老老实实的坐在自己的座位上,不能牵手。此时整体体系处于所有电子都不能动的状态,是个没有感情交流的绝缘态。
电子强关联导致的莫特态还有一个衍生的结果,就是自旋相反的电子倾向于交替排列,形成反铁磁结构。这里需要澄清一个很多人都可能有的误会,尤其是习惯第一性原理计算的朋友常常容易被误导。很多人觉得莫特态是电子反铁磁排列导致的结果,因为在需要用DFT+U做计算的时候,我们通常需要配合磁性来给特定局域轨道上添加轨道势。这其实只是第一性原理方法处理多体问题的一种不得已的方式,因为它本质上是一个单电子近似,没有办法真正处理多电子相互作用。严格定义的莫特态是不需要磁性长程序配合的,是纯粹的顺磁态电子关联效应。但是莫特态的出现,会使得体系倾向于衍生出反铁磁关联。所以,更准确的说,反铁磁应该是莫特态导致的结果,而不是原因。
其中的道理仍然可以用我们之前的比喻来进一步说明。两个年轻人原本感情很好,时刻都想拉拉手。但是长辈的存在,让他们不得不老老实实的坐在自己的位置上,这是我们前面说的莫特态。但是两个人的心思还都是想要拉手的,因此虽然面临的压力很大,但还是趁着长辈稍微不注意,偷偷摸摸的拉了一下,然后又快速的松开。两个人因为这次偷偷摸摸的拉手,感觉彼此的感情又进了一步。这种偷偷拉手的过程在不同自旋的电子间也会发生,我们称之为虚过程(virtual process)。如第一张图里所示,两个挨着的自旋相反的电子原本因为很强的库仑排斥没法稳定的移动到对方的位置上,但是这样的移动总是存在一定几率发生的。一旦发生,这两个电子会处于同一个态上,可以理解为两个年轻人牵上了手。
牵手的瞬间,两个电子感受到强大的库仑排斥力,就好像两个年轻人瞬间心跳加速,感觉时刻会被长辈发现一样,因此两个电子快速的分开,每个格点又重新变成了半占据的状况。如同两个年轻人短暂的牵手也会让彼此的感情更甜蜜一样,电子跃迁的虚过程可以使得这个体系基态的能量进一步降低。感兴趣的朋友可以尝试去对角化一下第一张图里的矩阵,得到的基态能量是比单占据的情形能量更低,因此这样的虚过程是倾向于发生的。由于这样的虚过程只能存在于自旋相反的两个电子间,因此电子就倾向于和周围的电子成自旋相反排列,从而出现反铁磁关联。为什么是反铁磁,而不是铁磁呢?因为如果是相同自旋的电子,他们之间因为泡利不相容原理,是无法发生虚跃迁过程的。对应着牵手过程…,来自于保守长辈的压力和原则性挑战可能更大一些吧。
轨道选择Mott转变
(Orbital-Selective Mott Transition)
理解了单轨道中的模特转变,我们再来尝试理解一下多轨道情形。我们同样用男女朋友的例子来解释。这里需要借助的不再是一对已经陷入热恋的男女,而是两只可怜的单身狗。在这之前,让我们先来看一下物理图像。实际固体材料的宏观物理特性主要是由费米面附近的电子决定的,因此我们常常需要去分析费米面的形状,了解费米面都是由哪些轨道成分构成的。大部分体系的费米面都是由超过一种轨道成分构成,我们在简化模型中只研究一条轨道显然是与实际情况相差太远。我们现在来考虑两条轨道的情形,这两条轨道都占据在费米面附近,并且假设他们都是半占据的,即它们各自有一半的态被占据了,一半的态还空着(费米面上下对应的面积是相同的)。我们假设这两个轨道稍微有点不同,不然,他们完全一摸一样的话就和单轨道的情形没有任何差别了。我们让他们一个胖一些,一个瘦一些。严谨点的说法是一个的带宽大一些,一个带宽小一些。我们可以把这两个轨道分别理解成两个单身的青年,带宽大一些的是一个胖子,带宽小一些的是个高富帅。在没有考虑电子相互作用的时候,两个人都是自由的单身狗,体系处于金属态,因为有空态和占据态可以互换。这时,我们慢慢的打开电子之间的相互作用,就好像两个人的家里开始慢慢的催促他们去找对象了。我们把从单身到结束单身理解成一个相变,把电子间关联的大小理解成为结束单身所付出的努力。那么当逐渐增大电子关联强度时,这两个轨道出现莫特相变的时间是不同的。带宽比较小的那个轨道会首先进入莫特态,在这个轨道中的电子会首先被固化下来;而带宽比较大的那个轨道会晚一些进入莫特态。当U足够的大的时候两者都可以发生莫特转变,都变成绝缘的。但是U存在一定的取值范围,使得带宽小的轨道是绝缘的,但是带宽大的轨道仍然是金属的。我们把这种莫特转变称之为轨道选择莫特转变,这是在单轨道体系中不会出现的新现象。为什么会出现分别先后进入莫特态的情况呢,电子间的相互作用明明是一样大小的呀。理解这一点,就要用到我们的两个单身青年做例子了。我们把U理解成了为结束单身而付出的努力。虽然两个人都付出了绝对值同样大小的努力,但是结束单身的效果显然对两个人来说是不同的。高富帅稍微付出一点努力,就很容易得到异性的青睐,结束单身生活,相变进入二人世界。然而,付出了同样大小的努力,胖青年收到的回报就要小很多。他不得不付出比高富帅多几倍的努力(更大的U值)才能找到另一半。用物理的语言来描述这一机制,其实就是作用在不同带宽轨道上的有效相互作用大小是不同的,真正决定什么时候发生莫特转变的是电子库仑势能与动能的比值,而不是库仑力的绝对强度。同样的U值,因为高富帅更瘦些,带宽窄,动能小,因此势能/动能的比值大,更容易发生莫特转变。上述介绍的轨道选择莫特转变机制其实是一个非常粗糙的图像,实际情况下还需要其他的条件配合才行。比如说需要两个不同带宽的轨道间的洪德耦合J的帮助,否则莫特转变也只会发生在相同的U值下[1, 2, 3]。轨道选择莫特转变也可以发生在相同带宽的多轨道体系中,但需要晶体场劈裂的配合[4, 5]。轨道选择莫特转变是一个神奇的转变,它的微观机制仍在不断的研究和理解过程中。其中保持金属性的轨道,也通常与普通的费米液体不同。轨道选择莫特转变也被认为是解释CaSrRuO4 [6]和铁基超导体 [7] 的一个重要理论图像。多轨道恰当填充Mott转变
(Multiorbital commensurate-filling Mott transition)
从单轨道扩展到多轨道后,相互作用的形式也变得更加丰富。除了电子之间感受到的库仑排斥力以外,不同轨道间还会受到洪德耦合的影响。前面我们聊过了洪德耦合J是形成轨道选择莫特转变的重要一环,其实它在多轨道体系中的效应不仅如此。这里我们介绍一个有趣的结果。洪德规则是大家在原子物理中学过的一个重要的知识点,它可以有效的帮助我们确定在未满壳层的原子或者离子基态电子组态及总角动量。基本的原则可以简单的描述为,电子倾向于以相同的自旋取向分别占据在不同的轨道上;即使做不到,也要优先满足这个分布规则。原子物理中我们接触到的都是孤立的原子,或者少数原子,体系通常都是绝缘的,由原子能级来描述。上述的孤立原子洪德规则通常都是适用的。但是对于未填满壳层中的迅游电子而言,我们对洪德规则的理解就很有限了,因为电子态不再是由原子中的简单能级来定义了,而是有一定宽度的能带,这时如何排布电子就是一个非平庸的问题。法国的Luca de’ Medici2011年利用动力学平均场首先研究了这个问题 [7],得到了一张颇有美学价值的相图。他研究的问题是在相同带宽的三轨道体系中,比如t2g轨道,在有洪德耦合的情况下,添加不同数目电子,金属绝缘体转变的行为。对于t2g而言,一共有三条轨道,最多可以填充6个电子。那么电子填充为3的情况对应于半满,显然是会有莫特相出现的。但是有趣的是,在其他整数填充的时候,体系也出现了绝缘态,只是需要的相互作用U远比半满时要大很多。并且相图关于半满对称,越远离半满的整数填充,发生莫特转变需要的U越大。整张相图看起来像是两张背对着的脸,作者用古罗马时期掌管转换(transition)的神Janus来形象的类比这张相图。Janus表示的是January,是每一年的开始。一张脸是望向过去,一张脸望向未来。整数填充的多轨道体系中出现金属绝缘体相变是一个有趣的发现,它丰富了我们对于莫特转变的理解。即,在非半满情况下,也可以出现莫特相。但是电子数N=2和N=4的时候,这个金属绝缘体转变视乎又与N=3情况不同。N=3时,用来表征金属和绝缘体转变的准粒子权重(可以理解为电子有效质量的倒数)从金属态中的有限值快速的减小为绝缘态中的零。而在N=2和N=4的时候,准粒子权重在U较大的参数范围内具有一个有限但是非常小的值。因此此时系统虽然处于金属态,却不同于正常的金属,是由洪德耦合导致的一种特别的非费米液体行为[5, 7],通常为被称为洪德金属。自旋轨道耦合体系中的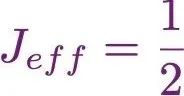 Mott态
Mott态
真实的材料体系中,尤其是对于由重元素构成的化合物中,自旋轨道耦合相互作用是一个不忽视的重要能量尺度,它对凝聚态物理的低能激发有重要的影响。我们通常都是在第一性原理计算中考虑自旋轨道耦合作用,在量子多体层次上理解它与电子关联、自旋涨落的竞争与配合是一件很复杂的事情。动力学平均场的局域近似使我们有机会去真正理解自旋轨道耦合的关联体系中的金属绝缘体相变。现在我们考虑在前述的t2g轨道中添加N=5个电子的情形,从Janus相图中我们可以看到我们需要施加非常大的U才能把体系变成绝缘态。但是物理学家们通过计算发现,其实有办法使得这个临界U值变小一点,只需要添加上一定的自旋轨道耦合。起初,这让人们有点疑惑。因此各种不同的能量尺度通常都是相互竞争的,为什么自旋轨道耦合这次会配合相互作用来诱导金属绝缘体相变呢?就像处理没有自旋轨道耦合的体系那样,让我们首先梳理一下有自旋轨道耦合后原子能级的排列[8]。在没有相互作用的孤立原子多轨道体系中,我们现在只有两个能量尺度。一个是晶体场劈裂,一个是自旋轨道耦合。让我们逐一把它施加到一个d电子的5个轨道上。通常情况下,晶体场劈裂的能量要远大于自旋轨道耦合的能量。我们这里考虑比较简单的立方晶体场的劈裂,它将5个d轨道劈裂成两组。一组含有3个轨道,称为t2g轨道;一组含有2个轨道,称为eg轨道。进一步考虑自旋轨道耦合的效应(原子物理老师正盯着你,千万别说不会算),t2g轨道会进一步劈裂成两个简并的Jeff=3/2的轨道和一条Jeff=1/2的轨道。而对于eg轨道,这里局域的自旋轨道耦合是不起作用的,要通过非局域的耦合配合一下才会出现微弱的自旋轨道耦合,标准的说法是eg轨道里的自旋轨道耦合是quenched的。如果此时在t2g轨道中添加5个电子,那么按照洪德耦合,Jeff=3/2的4个态被完全占据;Jeff=1/2的轨道里的两个态只有一个电子填充,属于半满情况。因此只需要一个比较小的相互作用就可以使体系变成绝缘态了[9, 10]。因为自旋轨道耦合效应的加入,在多轨道体系中能够出现的物理要远比莫特绝缘体丰富的多。这包括Jeff=1/2莫特绝缘体、非费米液体行为、拓扑绝缘体、复杂磁性、自旋液体等多种不同的微观行为。电子-电子关联与诸如晶体场劈裂、自旋轨道耦合等的相互竞争与配合,衍生出的各种新奇的物理相变和激发,得益于动力学平均场的局域近似简化,它使得我们研究多轨道系统中的不同能量尺度竞争成为了现实,极大的丰富了我们对于金属绝缘体相变的理解。
[1]. A. Koga, N. Kawakami, T. M. Rice, and M. Sigrist, Phys. Rev. Lett. 92, 216402 (2004)[2]. S. Biermann, L. de’ Medici, and A. Georges, Phys. Rev. Lett. 95, 206401 (2005)[3]. P. Werner and A.J. Millis, Phys. Rev. B 74, 155107 (2006)[4]. Luca de’ Medici, S. R. Hassan, Massimo Capone, and Xi Dai, Phys. Rev. Lett. 102, 126401 (2008)[5]. P. Werner and A. J. Millis. High-spin to low-spin and orbital polarization transitions in multiorbital Mott systems. Phys. Rev. Lett. 99, 126405 (2007)[6]. Anisimov, V. I., Nekrasov, I. A., Kondakov, D. E., Rice, T. M. & Sigrist, M. Orbital-selective Mott-insulator transition in Ca2−xSrxRuO4. Eur. Phys. J. B 25, 191–201 (2002)[7]. Luca de’ Medici, Gianluca Giovannetti, and Massimo Capone, Phys. Rev. Lett. 112, 177001(2012)[8]. G. Cao, L. De-Long, Book “Frontiers of 4d- and 5d-Transition metal Oxides” (2013)[9]. B. J. Kim, H. Jin, S.J. Moon, J.Y. Kim, B.G. Park, C.S. Leem, J. Yu, T. W. Noh, c. Kim, S. J. Oh, J.H. Park, V. Durairag and E. Rotenberg, Phys. Rev. Lett. 101, 076402, (2008) [10]. B.J. Kim, H. Ohsumi, T. Komesu, S. Sakai, T. Morita, H. Takagi and T. Arima, Science. 323, 1329 (2009)[11]. A. Biswas, K. Kim, and Y. Jeong, Book chapter in “Perovskite Materials - Synthesis, Characterisation, Properties, and Applications”. (2016)
本文系网易新闻·网易号“各有态度”特色内容
媒体转载联系授权请看下方

Mott态